What is the difference between node and antinode?
A node is a point on a standing wave where the amplitude is at its minimum. Think of it as the calmest point in the wave. On the other hand, an antinode is a point where the amplitude is at its maximum. You can picture this as the most energetic point in the wave.
Imagine a rope tied at one end and you’re shaking the other end. You’ll see a pattern of crests and troughs forming on the rope. The points where the rope barely moves are the nodes, and the points where the rope moves the most are the antinodes.
The nodes and antinodes are always alternating along a standing wave, and they are always directly opposite each other.
Think of it like this: nodes are where the wave’s energy is at its lowest, and antinodes are where the wave’s energy is at its highest.
Now, let’s explore how these concepts are applied in real-world scenarios:
Understanding Nodes and Antinodes in Music
Let’s say you have a guitar string. When you pluck the string, it vibrates, creating a standing wave. The points where the string doesn’t move are the nodes, and the points where the string vibrates with the greatest amplitude are the antinodes. The nodes are important in music because they help to determine the pitch and tone of a musical note.
Nodes and Antinodes in Radio Waves
Radio waves, a form of electromagnetic radiation, also have nodes and antinodes. Imagine a radio antenna transmitting a signal. The points where the signal is strongest are the antinodes, and the points where the signal is weakest are the nodes. This concept is crucial for understanding how radio waves travel and how radio receivers pick up signals.
Understanding the difference between nodes and antinodes can help you to better understand the behavior of waves and how they interact with their surroundings.
What is the distance between a node and another successive antinode?
Let’s break down why this is the case. A stationary wave, also known as a standing wave, is formed by the superposition of two waves traveling in opposite directions with the same frequency and amplitude. At certain points along the wave, the two waves interfere constructively, resulting in a maximum displacement called an antinode. At other points, the waves interfere destructively, leading to zero displacement called a node.
Imagine a rope tied at one end and being shaken up and down. The wave traveling down the rope will eventually reflect back from the fixed end, creating a wave traveling in the opposite direction. The superposition of these two waves forms a stationary wave pattern.
The distance between two successive nodes (or antinodes) is exactly half the wavelength. This is because the distance between a node and the next antinode is a quarter of the wavelength, and the distance between two successive antinodes (or nodes) is twice this distance, which is λ/2.
Understanding this relationship between nodes, antinodes, and wavelength is crucial for analyzing and understanding the behavior of stationary waves in various physical phenomena, like sound waves in musical instruments or light waves in lasers.
What is the distance between a node and antinode in a stationary wave is 20cm?
You’re right, the distance between a node and its nearest antinode in a stationary wave is λ/4, which is equal to 20 cm in this case. This means the wavelength (λ) of the wave is 80 cm (20 cm * 4 = 80 cm).
Now, to find the phase difference between two points separated by 60 cm, we need to consider the relationship between distance and phase in a stationary wave.
Here’s how we do it:
Phase Difference and Distance: The phase difference between two points on a wave is directly proportional to the distance between them. A full wavelength (λ) corresponds to a phase difference of 2π radians.
Calculating the Phase Difference:
* The distance between our two points is 60 cm, which is 3/4 of the wavelength (60 cm / 80 cm = 3/4).
* Since a full wavelength corresponds to a phase difference of 2π, a distance of 3/4 of a wavelength corresponds to a phase difference of (3/4) * 2π = 3π/2 radians.
So, the phase difference between two particles separated by 60 cm in a stationary wave with a 20 cm distance between a node and antinode is 3π/2 radians.
To understand this better, let’s visualize it:
Imagine a stationary wave as a rope tied at both ends and being vibrated. The points where the rope doesn’t move are nodes and the points where the rope vibrates with maximum amplitude are antinodes. The distance between a node and an antinode is always λ/4.
When you look at the wave, you’ll notice that the particles between two consecutive nodes or two consecutive antinodes are in phase (meaning they are moving in the same direction at the same time). However, the particles between a node and an antinode are out of phase.
In our example, two points separated by 60 cm would be located on opposite sides of an antinode. This means they are completely out of phase and have a phase difference of π radians or 3π/2 radians depending on which side of the antinode they are located.
Remember:
* A full wavelength (λ) is equal to 2π radians.
* The distance between a node and an antinode is λ/4.
* The phase difference is directly proportional to the distance between the points.
With this knowledge, you can easily calculate the phase difference between any two points on a stationary wave.
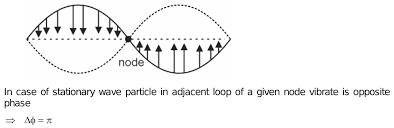
What is the phase difference between a node and an adjacent antinode?
Nodes are points on a wave where the amplitude is zero. Imagine a rope tied at both ends, and you give it a shake. The points where the rope doesn’t move are nodes. Antinodes are the points where the amplitude is maximum. They are the points where the rope swings the most.
Now, the phase difference between two consecutive antinodes is 180 degrees, meaning they are completely out of sync. Picture one antinode at its peak while the other is at its trough.
The key point here is that the phase difference between a node and an adjacent antinode is 90 degrees. This means that a node is at its minimum amplitude when the adjacent antinode is at its maximum amplitude, and vice versa.
Think of it like a clock. When the second hand points at 12, the minute hand is at its maximum (pointing towards 12). But when the second hand moves to 3, the minute hand is at its minimum (pointing towards 3). This 90-degree phase shift between the second and minute hands is similar to the relationship between a node and its neighboring antinode.
This phase difference of 90 degrees plays a crucial role in understanding wave behavior. For instance, in standing waves, which are formed when two identical waves traveling in opposite directions interfere, nodes and antinodes are fixed points. The distance between adjacent nodes or antinodes is half the wavelength of the wave.
Understanding the phase difference between nodes and antinodes helps us visualize and analyze wave phenomena. It’s like having a backstage pass to the fascinating world of waves, giving us a deeper understanding of their intricate dance.
What is the distance between node and antinode called?
Let’s break it down:
Wavelength: The wavelength of a wave is the distance between two consecutive nodes or two consecutive antinodes.
Distance between node and antinode: The distance between a node and an antinode is exactly half of the wavelength. This means if you know the wavelength, you can easily calculate the distance between a node and an antinode, and vice versa.
Now, let’s imagine a wave, like a wave on a string. Nodes are the points where the string doesn’t move at all. Think of them as the still points in the wave. Antinodes are the points where the string moves the most. They’re like the peaks and troughs of the wave.
If you were to measure the distance between a node and the nearest antinode, you would find it’s always exactly one-quarter of the wavelength. That’s because the distance between two consecutive nodes (or two consecutive antinodes) is one full wavelength, and the distance between a node and an antinode is half that distance.
This relationship between nodes, antinodes, and wavelength is crucial for understanding how waves behave. It helps us predict how waves will interact with each other and with different materials.
How to calculate nodes and antinodes?
You’re right, the amplitude of a standing wave can be represented by the equation 2a sin kx, where a is the amplitude.
Nodes are points where the amplitude is always zero. This means 2a sin kx = 0. To solve for k, we remember that the sine function equals zero at multiples of π. Therefore, kx = nπ, where n is an integer (0, 1, 2, 3,…). Since k = 2π/λ, where λ is the wavelength, we can substitute to find the positions of the nodes:
x = nλ/2
This means nodes occur at intervals of half a wavelength.
Antinodes, on the other hand, are points of maximum amplitude. In this case, 2a sin kx = 2a. This happens when sin kx = 1. The sine function reaches its maximum value of 1 at π/2, 3π/2, 5π/2…. Again, we can substitute k = 2π/λ to get the positions of the antinodes:
x = (2n + 1)λ/4
This means antinodes occur at intervals of half a wavelength, but shifted by a quarter of a wavelength from the nodes.
Let’s visualize this. Imagine a guitar string vibrating. The points where the string remains stationary are the nodes. These are the points where the waves interfere destructively, canceling each other out. The points where the string vibrates with the maximum amplitude are the antinodes. These are the points where the waves interfere constructively, reinforcing each other.
Remember, the distance between two consecutive nodes or two consecutive antinodes is always λ/2. The distance between a node and an adjacent antinode is λ/4.
By understanding these relationships and using the equations, you can easily calculate the positions of nodes and antinodes for any standing wave.
What is the shortest distance along the string between a node and an Antinode?
Let’s break down why this is:
Imagine a string vibrating. The string oscillates up and down, creating points of maximum displacement called antinodes and points of zero displacement called nodes. Think of it like a wave – the highest points are the peaks (antinodes), and the lowest points are the troughs (nodes).
Now, when we talk about the shortest distance between a node and an antinode, we’re looking for the most direct path. Since the wave pattern is repeating, the shortest distance isn’t along the entire length of the string. Instead, it’s the distance between the node and the antinode that are closest together.
Since nodes and antinodes alternate along the string, the space between a node and an antinode is always half the distance between two consecutive nodes or two consecutive antinodes. This is because the distance between two nodes is a full wavelength, and the distance between a node and an antinode is a quarter wavelength.
Think of it like a ruler – the space between two markings is a full unit, and the space between a marking and the midpoint is half a unit. The same principle applies to the distance between a node and an antinode on a vibrating string.
How to calculate the distance between nodes?
Dist(n1, n2) = Dist(root, n1) + Dist(root, n2) – 2*Dist(root, lca)
In this formula:
n1 and n2 represent the two nodes for which we want to find the distance.
root refers to the root node of the binary tree.
lca represents the lowest common ancestor of n1 and n2.
Let’s break down how this formula works. Imagine you have two nodes in a tree, and you want to find the shortest path between them. The path will always pass through their lowest common ancestor.
Dist(root, n1) gives you the distance from the root node to n1.
Dist(root, n2) gives you the distance from the root node to n2.
So, Dist(root, n1) + Dist(root, n2) represents the total distance from the root to each node. However, this includes the distance from the root to the LCA twice. To correct this, we subtract 2*Dist(root, lca).
Let’s illustrate with an example. Consider a binary tree with the following structure:
“`
A
/ \
B C
/ \ \
D E F
“`
Let’s say we want to find the distance between nodes D and F. The lowest common ancestor of D and F is A.
Here’s how we would apply the formula:
Dist(root, D) = 3 (the path is A -> B -> D)
Dist(root, F) = 2 (the path is A -> C -> F)
Dist(root, A) = 0 (the root is A itself)
Therefore, the distance between D and F would be:
Dist(D, F) = Dist(root, D) + Dist(root, F) – 2*Dist(root, A)
Dist(D, F) = 3 + 2 – 2 * 0
Dist(D, F) = 5
This calculation tells us that the shortest path between nodes D and F is 5 edges long.
What is the distance between node and antinode in a pipe open at both ends?
Let’s dive a little deeper into why this is the case. A standing wave is formed when two waves of the same frequency and amplitude travel in opposite directions and interfere with each other. At a node, the two waves interfere destructively, resulting in zero displacement. At an antinode, the two waves interfere constructively, resulting in maximum displacement.
The distance between a node and an antinode is exactly one-quarter of the wavelength. This is because the distance between two consecutive nodes or two consecutive antinodes is half a wavelength.
Now, let’s look at the statement: “A standing wave is produced in a string clamped at one end and free at the other end. The length of the string is odd multiples of λ/4.”
This statement is true. A string clamped at one end and free at the other end is an example of a system that can support standing waves. The fixed end of the string is a node, and the free end is an antinode. The length of the string must be an odd multiple of λ/4 to accommodate these boundary conditions. This is because the standing wave pattern must have a node at the fixed end and an antinode at the free end.
To illustrate, let’s consider the fundamental mode of vibration for a string clamped at one end and free at the other. In this mode, the string vibrates with one half-wavelength. The fixed end is a node, and the free end is an antinode. The length of the string is equal to λ/4.
The next higher mode of vibration has three half-wavelengths. The fixed end is a node, and the free end is an antinode. The length of the string is equal to 3λ/4.
And so on, for each higher mode of vibration, the length of the string is an odd multiple of λ/4.
See more here: What Is The Distance Between A Node And Another Successive Antinode? | Distance Between Node And Antinode
See more new information: countrymusicstop.com
Distance Between Node And Antinode | What Is The Difference Between Node And Antinode?
Understanding Nodes and Antinodes
Think of waves like a rope tied to a pole, shaking it up and down. Nodes are those spots where the rope stays perfectly still, while antinodes are the spots where the rope moves with the most amplitude—the highest peaks and deepest valleys.
This same concept applies to all kinds of waves, whether it’s sound waves vibrating in your ear, light waves reflecting off a mirror, or even water waves rippling in a pond.
The Distance Between a Node and an Antinode
The distance between a node and an antinode in any standing wave pattern is always a quarter wavelength (λ/4). It’s like a magical rule that always holds true.
Think of it this way:
* A node is a point of zero displacement, meaning the wave’s amplitude is zero at that point.
* An antinode is a point of maximum displacement, meaning the wave’s amplitude is at its peak.
The distance between these two points is exactly one-quarter of the total distance it takes for the wave to complete one full cycle, also known as the wavelength.
How to Calculate the Distance
Let’s say you’re looking at a standing wave on a string. You see a node at one end and an antinode at the other. If the total length of the string is ‘L’ and it represents half a wavelength (λ/2), then the distance between the node and the antinode is simply L/2.
Visualizing Nodes and Antinodes
Imagine a guitar string vibrating. You’ll notice certain spots on the string that remain still (nodes) while other spots vibrate with the largest amplitude (antinodes). This creates a pattern of nodes and antinodes, and the distance between each node and antinode is always a quarter wavelength.
Examples of Nodes and Antinodes
Here are a few more examples of nodes and antinodes in action:
Sound waves in a pipe: You can create a standing wave in a pipe by blowing across the open end. The closed end of the pipe will always be a node, and the open end will be an antinode.
Light waves in a laser cavity: The mirrors at the ends of a laser cavity reflect the light back and forth, creating standing waves. The mirrors are nodes, and the points in between are antinodes.
Why is this Important?
Understanding the relationship between nodes and antinodes is essential in many fields, including:
Music: Instruments like guitars, violins, and flutes rely on standing waves to produce their sounds. The positions of nodes and antinodes determine the fundamental frequency and the harmonics of the instrument.
Telecommunications: Microwave ovens and cell phone antennas use standing waves to transmit and receive signals. Understanding the positioning of nodes and antinodes is crucial for optimizing signal strength.
Physics: The concept of nodes and antinodes helps explain phenomena like interference and diffraction of waves.
FAQs
Q: How can I determine the position of nodes and antinodes in a wave?
A: You can determine the position of nodes and antinodes by observing the pattern of the wave. Nodes are the points where the wave’s amplitude is zero, while antinodes are the points where the amplitude is maximum.
Q: What is the difference between a node and an antinode?
A: A node is a point of zero displacement, meaning the wave’s amplitude is zero at that point. An antinode is a point of maximum displacement, meaning the wave’s amplitude is at its peak.
Q: Is the distance between two adjacent nodes always equal to half a wavelength?
A: Yes, the distance between two adjacent nodes or two adjacent antinodes is always equal to half a wavelength (λ/2).
Q: Can nodes and antinodes exist in both transverse and longitudinal waves?
A: Yes, nodes and antinodes can exist in both transverse waves (like waves on a string) and longitudinal waves (like sound waves).
Q: Why are nodes and antinodes important in music?
A: In music, the positions of nodes and antinodes determine the fundamental frequency and harmonics of an instrument. By manipulating the positions of nodes and antinodes, musicians can create different sounds and effects.
Hopefully, this information helps you understand the intriguing relationship between nodes and antinodes. Remember, the distance between a node and an antinode in a standing wave pattern is always a quarter wavelength (λ/4). It’s a fundamental concept that plays a vital role in understanding wave behavior across various fields.
Physics Tutorial: Nodes and Anti-nodes – The Physics Classroom
An antinode on the other hand is a point on the medium that is staying in the same location. Furthermore, an antinode vibrates back and forth between a large upward and a large downward displacement. And finally, nodes and antinodes are not actually part of The Physics Classroom
The distance between a node and an anti-node is – Toppr
The wavelength of a wave is defined as twice the distance between 2 consecutive nodes and antinodes. Now, the distance between an antinode and a node is 1/2 the distance Toppr
4.9.9 Nodes & Antinodes | OCR A Level Physics Revision Notes
Learn the definitions and properties of nodes and antinodes on a stationary wave. Find out how to calculate the wavelength from the distance between adjacent nodes or antinodes. savemyexams.com
Physics Tutorial: The Path Difference – The Physics Classroom
The nodes and anti-nodes lie along lines referred to as nodal and anti-nodal lines. The Path Difference refers to the difference in the distance traveled for a wave from one source to The Physics Classroom
8.8: Standing Waves – Physics LibreTexts
The distance between two neighboring nodes is half of a wavelength. The location where the wave oscillates away from equilibrium with double the amplitude of Physics LibreTexts
Standing Waves – Physics Book
The distance between the nodes is half the wavelength of the sound wave. Given that the distance between the heaps (which indicates the node distance) is 9.0 gatech.edu
Physics Tutorial: Closed-End Air Columns – The Physics Classroom
Since nodes always lie midway in between the antinodes, the distance between an antinode and a node must be equivalent to one-fourth of a wavelength. A careful analysis of the The Physics Classroom
16.6 Standing Waves and Resonance – OpenStax
In between each two nodes is an antinode, a place where the medium oscillates with an amplitude equal to the sum of the amplitudes of the individual waves. Consider two OpenStax
16.7: Standing Waves and Resonance – Physics LibreTexts
In between each two nodes is an antinode, a place where the medium oscillates with an amplitude equal to the sum of the amplitudes of the individual waves. Physics LibreTexts
Standing waves on strings (video) | Khan Academy
Use the distance between two consecutive nodes or two consecutive antinodes to calculate the length of a standing wave. Created by David SantoPietro. Questions. Tips & Thanks. Want to join the conversation? Log in. Sort by: Top Voted. Zoe. 8 years Khan Academy
The Distance Between Node And Antinode Is Equal To
The Distance Between Any Two Successive Nodes Or Antinodes In Stationary Waves Is
Nodes And Antinodes
Positions Of Nodes And Antinodes
The Distance Between Two Successive Nodes Or Antinodes Is Equal To
Link to this article: distance between node and antinode.
See more articles in the same category here: blog https://countrymusicstop.com/wiki
