Show That The Spherical Harmonics Are Eigenfunctions Of The Operator? New

Let’s discuss the question: “show that the spherical harmonics are eigenfunctions of the operator?” We summarize all relevant answers in section Q&A of website Countrymusicstop.com. See more related questions in the comments below.

Are spherical harmonics eigenfunctions of angular momentum?

The spherical harmonics play an important role in quantum mechanics. They are eigenfunctions of the operator of orbital angular momentum and describe the angular distribution of particles which move in a spherically-symmetric field with the orbital angular momentum l and projection m.

Keywords People Search

• show that the spherical harmonics are eigenfunctions of the operator
• SPHERICAL HARMONICS | Quantum Theory of Angular Momentum

show that the spherical harmonics are eigenfunctions of the operator – The spherical harmonics

Watch Video Now

Pictures on the topic show that the spherical harmonics are eigenfunctions of the operator | The spherical harmonics

How do you find spherical harmonics?

ℓ (θ, φ) = ℓ(ℓ + 1)Y m ℓ (θ, φ) . That is, the spherical harmonics are eigenfunctions of the differential operator L2, with corresponding eigenvalues ℓ(ℓ + 1), for ℓ = 0, 1, 2, 3,…. aℓmδℓℓ′ δmm′ = aℓ′m′ .

Keywords People Search

• show that the spherical harmonics are eigenfunctions of the operator
• The Spherical Harmonics

How do you find eigenvalues and eigenfunctions of an operator?

Updating

Keywords People Search

• show that the spherical harmonics are eigenfunctions of the operator
• Quantum Chemistry 3.3 – Eigenvalues and Eigenfunctions – YouTube

How do you determine if a wave function is an eigenfunction of an operator?

If the operator for a particular observable O operates on a wave function ψ(x,t), and the result of this operation is the wave function ψ(x,t) multiplied by a constant, then the wave function is said to be an eigenfunction of the operator and the constant one of its eigenvalues.

Keywords People Search

• show that the spherical harmonics are eigenfunctions of the operator
• Predictions

What are the eigenfunctions of angular momentum?

The spherical harmonics therefore are eigenfunctions of ˆM2 with eigenvalues given by Equation 7.4. 2, where J is the angular momentum quantum number. The magnitude of the angular momentum, i.e. the length of the angular momentum vector, √M2, varies with the quantum number J. 22 thg 7, 2021

Keywords People Search

• Are spherical harmonics eigenfunctions of angular momentum?
• 7.4: Angular Momentum Operators and Eigenvalues

What are eigenfunctions and eigenvalues?

An eigenfunction of an operator is a function such that the application of on gives. again, times a constant. (49) where k is a constant called the eigenvalue. It is easy to show that if is a linear operator with an eigenfunction , then any multiple of is also an eigenfunction of .

Keywords People Search

• Are spherical harmonics eigenfunctions of angular momentum?
• Eigenfunctions and Eigenvalues

What are spherical harmonic functions?

Spherical harmonics are a set of functions used to represent functions on the surface of the sphere S 2 S^2 S2. They are a higher-dimensional analogy of Fourier series, which form a complete basis for the set of periodic functions of a single variable (functions on the circle. S^1).

Keywords People Search

• How do you find spherical harmonics?
• Spherical Harmonics | Brilliant Math & Science Wiki

What are spherical harmonic coefficients?

The spherical harmonics are the angular portion of the solution to Laplace’s equation in spherical coordinates where azimuthal symmetry is not present.

Keywords People Search

• How do you find spherical harmonics?
• Spherical Harmonic — from Wolfram MathWorld

Where are spherical harmonics used?

Spherical harmonics are important in many theoretical and practical applications, including the representation of multipole electrostatic and electromagnetic fields, electron configurations, gravitational fields, geoids, the magnetic fields of planetary bodies and stars, and the cosmic microwave background radiation.

Keywords People Search

• How do you find spherical harmonics?
• Spherical harmonics – Wikipedia

How do you find eigenfunctions?

You can check for something being an eigenfunction by applying the operator to the function, and seeing if it does indeed just scale it. You find eigenfunctions by solving the (differential) equation Au = au. Notice that you are not required to find an eigenfunction- you are already given it. 3 thg 9, 2007

Keywords People Search

• How do you find eigenvalues and eigenfunctions of an operator?
• Eigenfunction of an Operator | Physics Forums

Which of the following are eigenfunctions of the momentum operator?

Ψ(x) is the eigenfunction of the momentum operator with the eigenvalue λ = − ℏ k \lambda = -\hbar k λ=−ℏk. 4 thg 6, 2021

Keywords People Search

• How do you find eigenvalues and eigenfunctions of an operator?
• Answer to Question #203210 in Physics for Vinod Kumar

How do you calculate eigenfunctions?

Updating

Keywords People Search

• How do you find eigenvalues and eigenfunctions of an operator?
• Eigenfunctions and Eigenvalues – YouTube

Which of the following wave functions are eigenfunctions of the operator d2 dx2?

cos(3x) is an eigenfunction of the operator d2/dx2.

Keywords People Search

• How do you determine if a wave function is an eigenfunction of an operator?
• The foundations of quantum mechanics

Is the wave function an eigenfunction of the Hamiltonian?

A system prepared in a superpostion state may have wavefunction (assuming each are already normalized.) In this case is not an eigenfunction of the Hamiltonian. In general, the set of eigenfunctions of an operator can be used as a basis set. Any wavefunction can. 30 thg 6, 2012

Keywords People Search

• How do you determine if a wave function is an eigenfunction of an operator?
• Eigenfunction vs wave function | Physics Forums

Is eigenfunction the same as eigenstate?

An eigenstate is a vector in the Hilbert space of a system, things we usually write like | >. An eigenfunction is an element of the space of functions on some space, which forms a vector space since you can add functions (pointwise) and multiply them by constants. 25 thg 2, 2009

Keywords People Search

• How do you determine if a wave function is an eigenfunction of an operator?
• What the differ between eigenstate and eigenfunction ? | Physics Forums

What are simultaneous eigenfunctions?

The simultaneous eigenfunctions of L2 and Lz are the spherical harmonics Ylm(θ, φ) and the simultaneous eigenfunctions of S2 and Sz are |SMs〉 with S = 1 and Ms = 1,0, − 1. From: Atoms and Molecules, 1978.

Keywords People Search

• What are the eigenfunctions of angular momentum?
• Simultaneous Eigenfunctions – an overview | ScienceDirect Topics

What is total angular momentum operator?

In simpler terms, the total angular momentum operator characterizes how a quantum system is changed when it is rotated. The relationship between angular momentum operators and rotation operators is the same as the relationship between Lie algebras and Lie groups in mathematics, as discussed further below.

Keywords People Search

• What are the eigenfunctions of angular momentum?
• Angular momentum operator – Wikipedia

How do you find eigenvalues of angular momentum operator?

Updating

Keywords People Search

• What are the eigenfunctions of angular momentum?
• Angular momentum eigenvalues – YouTube

What do you mean by eigenfunctions?

In mathematics, an eigenfunction of a linear operator D defined on some function space is any non-zero function in that space that, when acted upon by D, is only multiplied by some scaling factor called an eigenvalue.

Keywords People Search

• What are eigenfunctions and eigenvalues?
• Eigenfunction – Wikipedia

Which of the following functions are eigenfunctions of the operator D DX?

Which of the following is Eigen function of D DX? The function eax is aneigenfunction of the operator d/dx because (d/dx)eax ¼ aeax, which is a constant (a) multiplying the original function. … The constant o in an eigenvalueequation is called theeigenvalue of the operator O. 22 thg 12, 2020

Keywords People Search

• What are eigenfunctions and eigenvalues?
• which of the following functions are eigen functions of d2/dx2. 1). Sin3x.

What are the eigenstates and eigenvalues of the Hamiltonian?

When discussing the eigenstates of the Hamiltonian (ˆH), the associated eigenvalues represent energies and within the context of the momentum operators, the associated eigenvalues refer to the momentum of the particle. 8 thg 9, 2021

Keywords People Search

• What are eigenfunctions and eigenvalues?
• 3.3: The Schrödinger Equation is an Eigenvalue Problem

What is spherical harmonics in chemistry?

Spherical Harmonics are a group of functions used in math and the physical sciences to solve problems in disciplines including geometry, partial differential equations, and group theory. The general, normalized Spherical Harmonic is depicted below: Yml(θ,ϕ)=√(2l+1)(l−|m|)! 14 thg 11, 2020

Keywords People Search

• What are spherical harmonic functions?
• Spherical Harmonics – Chemistry LibreTexts

Are spherical harmonics symmetric?

The spherical harmonics are often represented graphically since their linear combinations correspond to the angular functions of orbitals. Figure 1.1a shows a plot of the spherical harmonics where the phase is color coded. One can clearly see that is symmetric for a rotation about the z axis.

Keywords People Search

• What are spherical harmonic functions?
• 1 Properties of Spherical Harmonics

What is a spherical harmonic degree?

Spherical harmonics are the spherical analogue of trigonometric polynomials on [−π,π). The degree ℓ≥0, order m (−ℓ≤m≤m) spherical harmonic is denoted by Ymℓ(λ,θ), and can be expressed (in real form) as [1, Sec.

Keywords People Search

• What are spherical harmonic functions?
• Spherical harmonics – Chebfun

Are spherical harmonics real?

Real spherical harmonics (RSH) are obtained by combining complex conjugate functions associated to opposite values of . RSH are the most adequate basis functions for calculations in which atomic symmetry is important since they can be directly related to the irreducible representations of the subgroups of [Blanco1997].

Keywords People Search

• What are spherical harmonic coefficients?
• Complex and Real Spherical Harmonics – abinit

What does it mean for a function to be harmonic?

harmonic function, mathematical function of two variables having the property that its value at any point is equal to the average of its values along any circle around that point, provided the function is defined within the circle.

Keywords People Search

• Where are spherical harmonics used?
• harmonic function | mathematics – Encyclopedia Britannica

How do you decompose a function into spherical harmonics?

If you have a function f(x), you can decompose it as an infinite sum of sine waves of the form sin(nx) and cos(nx) for increasing n. If you have a function g(theta,phi), you can decompose it into spherical harmonics; for each order l you have 2l+1 spherical harmonics. 26 thg 9, 2007

Keywords People Search

• Where are spherical harmonics used?
• Spherical harmonic decomposition | Physics Forums

How do you find the eigenvalue of an operator?

For a given linear operator T : V → V , a nonzero vector x and a constant scalar λ are called an eigenvector and its eigenvalue, respec- tively, when T(x) = λx. For a given eigenvalue λ, the set of all x such that T(x) = λx is called the λ-eigenspace.

Keywords People Search

• How do you find eigenfunctions?
• Eigenvalues, eigenvectors, and eigenspaces of linear operators …

What are the eigenfunctions and eigenvalues of the momentum operator?

If the momentum operator operates on a wave function and IF AND ONLY IF the result of that operation is a constant multiplied by the wave function, then that wave function is an eigenfunction or eigenstate of the momentum operator, and its eigenvalue is the momentum of the particle.

Keywords People Search

• Which of the following are eigenfunctions of the momentum operator?
• basics of quantum mechanics – Oregon State University

What is the momentum for a particle trapped in a box?

3.7: The Average Momentum of a Particle in a Box is Zero – Chemistry LibreTexts. 18 thg 3, 2020

Keywords People Search

• Which of the following are eigenfunctions of the momentum operator?
• 3.7: The Average Momentum of a Particle in a Box is Zero

What is momentum operator squared?

In position space, the momentum operator in 1D is ˆp=ℏi∂∂x. Squaring this would be ˆp2=ℏ2i2∂2∂x2. Using the superposition principle, in which x and y components of the momentum are uncorrelated, we arrive at the same result you obtained. 7 thg 5, 2018

Keywords People Search

• Which of the following are eigenfunctions of the momentum operator?
• What is square of momentum operator $\hat{P}$ in two dimensions?

Can eigenfunctions be imaginary?

The eigenfunctions of a Hermitian operator are real. But consider a function ψ(x)=e−κx, x∈R, where κ is a real constant. Then, ˆpψ(x)=−iℏddxe−κx=iκℏψ(x). This gives a pure imaginary eigenvalue. 12 thg 2, 2014

Keywords People Search

• How do you calculate eigenfunctions?
• Imaginary Eigenvalue Of A Hermitian Operator – Physics Stack Exchange

How do you calculate normalized eigenfunctions?

Updating

Keywords People Search

• How do you calculate eigenfunctions?
• Diff Eqn: Finding normalized eigenfunctions of a bvp – YouTube

How do you find eigenfunctions in Sturm Liouville?

(p(x)y′)′ + (q(x) + λr(x))y = 0, a < x < b, (plus boundary conditions), is called an eigenfunction, and the corresponding value of λ is called its eigenvalue. The eigenvalues of a Sturm-Liouville problem are the values of λ for which nonzero solutions exist. 10 thg 4, 2012

Keywords People Search

• How do you calculate eigenfunctions?
• Introduction to Sturm-Liouville Theory – Trinity University

Is D DX a linear operator?

However d/dx is considered to be a linear operator. If I understand this correctly, that means we have to convert the function we are taking the derivative of into a vector that represents it. The linear operator then maps the vector to another vector which represents a new polynomial. 9 thg 8, 2019

Keywords People Search

• Which of the following wave functions are eigenfunctions of the operator d2 dx2?
• The Derivative of a Linear Operator – calculus – Math Stack Exchange

Which of the following wave function is the solution of Schrödinger equation?

The wave function Ψ(x, t) = Aei(kx−ωt) represents a valid solution to the Schrödinger equation. The wave function is referred to as the free wave function as it represents a particle experiencing zero net force (constant V ).

Keywords People Search

• Which of the following wave functions are eigenfunctions of the operator d2 dx2?
• 4 The Schrödinger wave equation

What is the physical significance of wave function and ψ2?

ψ is a wave function and refers to the amplitude of electron wave i.e. probability amplitude. It has got no physical significance. The wave function ψ may be positive, negative or imaginary. [ψ]2 is known as probability density and determines the probability of finding an electron at a point within the atom.

Keywords People Search

• Which of the following wave functions are eigenfunctions of the operator d2 dx2?
• significance of ψ and ψ2 in … | Homework Help | myCBSEguide

What is the expression of Hamiltonian operator?

The Hamiltonian operator, H ^ ψ = E ψ , extracts eigenvalue E from eigenfunction ψ, in which ψ represents the state of a system and E its energy. The expression H ^ ψ = E ψ is Schrödinger’s time-independent equation.

Keywords People Search

• Is the wave function an eigenfunction of the Hamiltonian?
• Hamiltonian Operator – an overview | ScienceDirect Topics

Are wave functions eigenfunctions?

A wave function is an object representing the quantum state of a system. An eigenfunction is a function with a definite observable value of some corresponding operator.

Keywords People Search

• Is the wave function an eigenfunction of the Hamiltonian?
• What is the difference between wave function and eigenfunction? – Quora

What kind of operator is the Hamiltonian?

In quantum mechanics, the Hamiltonian of a system is an operator corresponding to the total energy of that system, including both kinetic energy and potential energy.

Keywords People Search

• Is the wave function an eigenfunction of the Hamiltonian?
• Hamiltonian (quantum mechanics) – Wikipedia

What is the eigen value when the eigen function EX * is operated on the operator D DX?

a^ne^x is the eigen value of the function e^ax when operated on the operator d^n/dx^n. 19 thg 10, 2020

Keywords People Search

• Is eigenfunction the same as eigenstate?
• What is the eigen value of the function e^ax when operated on … – Brainly.in

When two operators commute What can we say about their eigenfunctions?

If two operators commute and consequently have the same set of eigenfunctions, then the corresponding physical quantities can be evaluated or measured exactly simultaneously with no limit on the uncertainty. 18 thg 3, 2020

Keywords People Search

• What are simultaneous eigenfunctions?
• 4.6: Commuting Operators Allow Infinite Precision

What is a simultaneous Eigenket?

It means that you can write and , which means is the eigenket of both A and B, so their “simultaneous eigenket”! Reply. 12 thg 2, 2015

Keywords People Search

• What are simultaneous eigenfunctions?
• Simultaneous Eigenkets? | Physics Forums

How do you show two operators commute?

Updating

Keywords People Search

• What are simultaneous eigenfunctions?
• Quantum Mechanics | Commutation of Operators [Example #2] – YouTube

What is ordinary angular momentum?

In physics, angular momentum (rarely, moment of momentum or rotational momentum) is the rotational analog of linear momentum. It is an important quantity in physics because it is a conserved quantity—the total angular momentum of a closed system remains constant.

Keywords People Search

• What is total angular momentum operator?
• Angular momentum – Wikipedia

How do you find the orbital angular momentum?

quantum numbers giving the total orbital angular momentum and total spin angular momentum of a given state. The total orbital angular momentum is the sum of the orbital angular momenta from each of the electrons; it has magnitude Square root of√L(L + 1) (ℏ), in which L is an integer.

Keywords People Search

• What is total angular momentum operator?
• orbital angular momentum | physics | Britannica

What is generalized angular momentum?

A generalized angular momentum (i.e., one that may include spin) is defined as any vector operator whose components obey the commutation relations of Eqs.

Keywords People Search

• What is total angular momentum operator?
• Quantum Mechanics of Angular Momentum – Wiley Online Library

What is the eigenfunction of the orbital angular momentum operator?

The orbital angular momentum operator in Cartesian coordinate has the form L = r × p. We check if (y – iz)k is an eigenfunction of Lx = ypz – zpy = (ħ/i)(y∂/∂z – z∂/∂y).

Keywords People Search

• How do you find eigenvalues of angular momentum operator?
• Orbital angular momentum

What is the eigen function of angular momentum?

The spherical harmonics therefore are eigenfunctions of ˆM2 with eigenvalues given by Equation 7.4. 2, where J is the angular momentum quantum number. The magnitude of the angular momentum, i.e. the length of the angular momentum vector, √M2, varies with the quantum number J. 22 thg 7, 2021

Keywords People Search

• How do you find eigenvalues of angular momentum operator?
• 7.4: Angular Momentum Operators and Eigenvalues

How do you find eigenvalues in quantum mechanics?

Updating

Keywords People Search

• How do you find eigenvalues of angular momentum operator?
• Eigenvalues and eigenstates in quantum mechanics – YouTube

What is meant by eigenfunctions and eigenvalues?

An eigenfunction of an operator is a function such that the application of on gives. again, times a constant. (49) where k is a constant called the eigenvalue. It is easy to show that if is a linear operator with an eigenfunction , then any multiple of is also an eigenfunction of .

Keywords People Search

• What do you mean by eigenfunctions?
• Eigenfunctions and Eigenvalues

What are eigenfunctions and eigenvalues in chemistry?

When an operator operating on a function results in a constant times the function, the function is called an eigenfunction of the operator & the constant is called the eigenvalue. i.e. A f(x) = k f(x) where f(x) is the eigenfunction & k is the eigenvalue. 11 thg 10, 2011

Keywords People Search

• What do you mean by eigenfunctions?
• what is the eigen value and eigen function – Chemistry | 40j1tell

What do you mean by eigenfunctions and eigenvalues in physics?

In the case of Schrodinger’s equation, the eigenvalues are the possible energies that the system can have if it is in a state of well-defined energy. Each eigenfunction (of the Hamiltonian) is the state of the system when its energy is equal to the associated eigenvalue. 6 thg 12, 2018

Keywords People Search

• What do you mean by eigenfunctions?
• What is eigenvalue and eigenfunction in quantum mechanics?

Which of the following are eigenfunctions for the operator d2 dx2?

cos(3x) is an eigenfunction of the operator d2/dx2.

Keywords People Search

• Which of the following functions are eigenfunctions of the operator D DX?
• The foundations of quantum mechanics

Is K an eigenfunction of D DX?

How many different eigenfunctions are there for the operator d/dx? Since there are no restrictions on k, there are an infinite number of eigenfunctions of d/dx of this form.

Keywords People Search

• Which of the following functions are eigenfunctions of the operator D DX?
• notes_Ch3.pdf

What are the operators?

In mathematics and sometimes in computer programming, an operator is a character that represents an action, as for example x is an arithmetic operator that represents multiplication. In computer programs, one of the most familiar sets of operators, the Boolean operators, is used to work with true/false values.

Keywords People Search

• Which of the following functions are eigenfunctions of the operator D DX?
• What is operator? – Definition from WhatIs.com

What are the eigenstates of the Hamiltonian?

A system prepared in an eigenstate of the Hamiltonian has time-invariant probability density. A system prepared in an eigenstate of a non-commuting operator has a probability density which varies in time. It is this time independence (conservation law) which makes eigenstates of the energy operator so useful.

Keywords People Search

• What are the eigenstates and eigenvalues of the Hamiltonian?
• 1 Summary of things you should already know

Are eigenvectors and Eigenstates the same?

is that eigenvector is (linear algebra) a vector that is not rotated under a given linear transformation; a left or right eigenvector depending on context while eigenstate is (physics) a dynamic quantum mechanical state whose wave function is an eigenvector that corresponds to a physical quantity.

Keywords People Search

• What are the eigenstates and eigenvalues of the Hamiltonian?
• Eigenvector vs Eigenstate – What’s the difference? | WikiDiff

What are Eigenstates?

Definition of eigenstate : a state of a quantized dynamic system (such as an atom, molecule, or crystal) in which one of the variables defining the state (such as energy or angular momentum) has a determinate fixed value.

Keywords People Search

• What are the eigenstates and eigenvalues of the Hamiltonian?
• Eigenstate Definition & Meaning – Merriam-Webster

What are spherical harmonic functions?

Spherical harmonics are a set of functions used to represent functions on the surface of the sphere S 2 S^2 S2. They are a higher-dimensional analogy of Fourier series, which form a complete basis for the set of periodic functions of a single variable (functions on the circle. S^1).

Keywords People Search

• What is spherical harmonics in chemistry?
• Spherical Harmonics | Brilliant Math & Science Wiki

Where are spherical harmonics used?

Spherical harmonics are important in many theoretical and practical applications, including the representation of multipole electrostatic and electromagnetic fields, electron configurations, gravitational fields, geoids, the magnetic fields of planetary bodies and stars, and the cosmic microwave background radiation.

Keywords People Search

• What is spherical harmonics in chemistry?
• Spherical harmonics – Wikipedia

What are spherical harmonic coefficients?

The spherical harmonics are the angular portion of the solution to Laplace’s equation in spherical coordinates where azimuthal symmetry is not present.

Keywords People Search

• Are spherical harmonics symmetric?
• Spherical Harmonic — from Wolfram MathWorld

How do you find spherical harmonics?

ℓ (θ, φ) = ℓ(ℓ + 1)Y m ℓ (θ, φ) . That is, the spherical harmonics are eigenfunctions of the differential operator L2, with corresponding eigenvalues ℓ(ℓ + 1), for ℓ = 0, 1, 2, 3,….

Keywords People Search

• Are spherical harmonics symmetric?
• The Spherical Harmonics

What is spherical harmonics in chemistry?

Spherical Harmonics are a group of functions used in math and the physical sciences to solve problems in disciplines including geometry, partial differential equations, and group theory. The general, normalized Spherical Harmonic is depicted below: Yml(θ,ϕ)=√(2l+1)(l−|m|)! 14 thg 11, 2020

Keywords People Search

• What is a spherical harmonic degree?
• Spherical Harmonics – Chemistry LibreTexts

What is spherical harmonics in quantum mechanics?

The spherical harmonics play an important role in quantum mechanics. They are eigenfunctions of the operator of orbital angular momentum and describe the angular distribution of particles which move in a spherically-symmetric field with the orbital angular momentum l and projection m.

Keywords People Search

• What is a spherical harmonic degree?
• SPHERICAL HARMONICS | Quantum Theory of Angular Momentum

Are spherical harmonics Orthonormal?

Updating

Keywords People Search

• Are spherical harmonics real?
• Orthonormality of spherical harmonics – YouTube

Are spherical harmonics symmetric?

The spherical harmonics are often represented graphically since their linear combinations correspond to the angular functions of orbitals. Figure 1.1a shows a plot of the spherical harmonics where the phase is color coded. One can clearly see that is symmetric for a rotation about the z axis.

Keywords People Search

• Are spherical harmonics real?
• 1 Properties of Spherical Harmonics

How do you show a harmonic function?

If f(z) = u(x, y) + iv(x, y) is analytic on a region A then both u and v are harmonic functions on A. Proof. This is a simple consequence of the Cauchy-Riemann equations.

Keywords People Search

• What does it mean for a function to be harmonic?
• Topic 5 Notes 5 Introduction to harmonic functions

Why are harmonic functions called harmonic?

The descriptor “harmonic” in the name harmonic function originates from a point on a taut string which is undergoing harmonic motion. The solution to the differential equation for this type of motion can be written in terms of sines and cosines, functions which are thus referred to as harmonics.

Keywords People Search

• What does it mean for a function to be harmonic?
• Harmonic function – Wikipedia

Are spherical harmonics complex?

Real spherical harmonics (RSH) are obtained by combining complex conjugate functions associated to opposite values of .

Keywords People Search

• How do you decompose a function into spherical harmonics?
• Complex and Real Spherical Harmonics – abinit

What does it mean for a function to be harmonic?

harmonic function, mathematical function of two variables having the property that its value at any point is equal to the average of its values along any circle around that point, provided the function is defined within the circle.

Keywords People Search

• How do you decompose a function into spherical harmonics?
• harmonic function | mathematics – Encyclopedia Britannica

How do you find eigenvalues and eigenfunctions of an operator?

Updating

Keywords People Search

• How do you find the eigenvalue of an operator?
• Quantum Chemistry 3.3 – Eigenvalues and Eigenfunctions – YouTube

How do you find the eigenvalues of a Hamiltonian matrix?

To find the eigenvalues E we set the determinant of the matrix (H – EI) equal to zero and solve for E. To find the corresponding eigenvectors {|Ψ>}, we substitute each eigenvalue E back into the equation (H-E*I)|Ψ> = 0 and solve for the expansion coefficients of |Ψ> in the given basis.

Keywords People Search

• How do you find the eigenvalue of an operator?
• Eigenvalues

Which of the following are eigenfunctions of the momentum operator?

Ψ(x) is the eigenfunction of the momentum operator with the eigenvalue λ = − ℏ k \lambda = -\hbar k λ=−ℏk. 4 thg 6, 2021

Keywords People Search

• What are the eigenfunctions and eigenvalues of the momentum operator?
• Answer to Question #203210 in Physics for Vinod Kumar

What is momentum operator squared?

In position space, the momentum operator in 1D is ˆp=ℏi∂∂x. Squaring this would be ˆp2=ℏ2i2∂2∂x2. Using the superposition principle, in which x and y components of the momentum are uncorrelated, we arrive at the same result you obtained. 7 thg 5, 2018

Keywords People Search

• What are the eigenfunctions and eigenvalues of the momentum operator?
• What is square of momentum operator $\hat{P}$ in two dimensions?

What is the expectation value of momentum of a particle trapped in a one dimensional box?

The reason that the average momentum comes out to zero because momentum is a vector quantity and the particle is as much likely to be moving to the left and the right so that the average value of momentum is zero. 25 thg 1, 2020

Keywords People Search

• What is the momentum for a particle trapped in a box?
• Why is the expectation value of momentum of a particle in an …

What is meant by quantum tunneling?

Definition of quantum tunneling A quantum mechanical effect in which particles have a finite probability of crossing an energy barrier, such as the energy needed to break a bond with another particle, even though the particle’s energy is less than the energy barrier.

Keywords People Search

• What is the momentum for a particle trapped in a box?
• Quantum tunneling Definition & Meaning | Dictionary.com

What is linear momentum operator?

The Linear Momentum Operator is the quantum mechanical operator which gives an instruction to differentiate with respect to x (position) and multiply by −iℏ.

Keywords People Search

• What is momentum operator squared?
• Linear Momentum Operator | Quatomic

Which operator is associated with momentum?

The Hamiltonian Operator Name Observable Symbol Operator Symbol Momentum (in 3D) →p ˆP Kinetic Energy (in 1D) Tx ^Tx Kinetic Energy (in 3D) T ˆT Potential Energy (in 1D) V(x) ˆV(x) 8 hàng khác • 8 thg 9, 2021

Keywords People Search

• What is momentum operator squared?
• 4.2: Quantum Operators Represent Classical Variables

What do you mean by eigenfunctions?

In mathematics, an eigenfunction of a linear operator D defined on some function space is any non-zero function in that space that, when acted upon by D, is only multiplied by some scaling factor called an eigenvalue.

Keywords People Search

• Can eigenfunctions be imaginary?
• Eigenfunction – Wikipedia

How do you show eigenfunctions are orthogonal?

Multiply the first equation by φ∗ and the second by ψ and integrate. If a1 and a2 in Equation 4.5. 14 are not equal, then the integral must be zero. This result proves that nondegenerate eigenfunctions of the same operator are orthogonal. 18 thg 3, 2020

Keywords People Search

• Can eigenfunctions be imaginary?
• 4.5: Eigenfunctions of Operators are Orthogonal – Chemistry LibreTexts

Which of the following functions are eigenfunctions of the operator D DX?

Which of the following is Eigen function of D DX? The function eax is aneigenfunction of the operator d/dx because (d/dx)eax ¼ aeax, which is a constant (a) multiplying the original function. … The constant o in an eigenvalueequation is called theeigenvalue of the operator O. 22 thg 12, 2020

Keywords People Search

• Can eigenfunctions be imaginary?
• which of the following functions are eigen functions of d2/dx2. 1). Sin3x.

How are the eigenfunctions and eigenvalues related to the Sturm-Liouville problem?

(p(x)y′)′ + (q(x) + λr(x))y = 0, a < x < b, (plus boundary conditions), is called an eigenfunction, and the corresponding value of λ is called its eigenvalue. The eigenvalues of a Sturm-Liouville problem are the values of λ for which nonzero solutions exist. 10 thg 4, 2012

Keywords People Search

• How do you find eigenfunctions in Sturm Liouville?
• Introduction to Sturm-Liouville Theory – Trinity University

What makes a Sturm-Liouville problem?

(In the case of more general p(x), q(x), w(x), the solutions must be understood in a weak sense.) In addition, y is typically required to satisfy some boundary conditions at a and b. Each such equation (1) together with its boundary conditions constitutes a Sturm–Liouville (S-L) problem.

Keywords People Search

• How do you find eigenfunctions in Sturm Liouville?
• Sturm–Liouville theory – Wikipedia

How do you solve the strum Louville problem?

These equations give a regular Sturm-Liouville problem. Identify p,q,r,αj,βj in the example above. y(x)=Acos(√λx)+Bsin(√λx)if λ>0,y(x)=Ax+Bif λ=0. Let us see if λ=0 is an eigenvalue: We must satisfy 0=hB−A and A=0, hence B=0 (as h>0), therefore, 0 is not an eigenvalue (no nonzero solution, so no eigenfunction). 12 thg 2, 2022

Keywords People Search

• How do you find eigenfunctions in Sturm Liouville?
• 5.1: Sturm-Liouville problems – Mathematics LibreTexts

Is √ a linear operator?

16) hold? Condition B does not hold, therefore the square root operator is not linear. The most operators encountered in quantum mechanics are linear operators. 5 thg 12, 2019

Keywords People Search

• Is D DX a linear operator?
• 3.2: Linear Operators in Quantum Mechanics – Chemistry LibreTexts

How do you show an operator is linear?

A function f is called a linear operator if it has the two properties: f(x+y)=f(x)+f(y) for all x and y; f(cx)=cf(x) for all x and all constants c.

Keywords People Search

• Is D DX a linear operator?
• Linear operator | Glossary | Underground Mathematics

How do you find the linear operator?

Updating

Keywords People Search

• Is D DX a linear operator?
• Linear Operators Part 1 – YouTube

What does solving Schrodinger equation mean?

Solving the Schrodinger equation means finding the ​quantum mechanical wave function​ that satisfies it for a particular situation. 28 thg 12, 2020

Keywords People Search

• Which of the following wave function is the solution of Schrödinger equation?
• Schrodinger’s Equation: Explained & How to Use It – Sciencing

How do you find the Schrodinger equation?

Updating

Keywords People Search

• Which of the following wave function is the solution of Schrödinger equation?
• SOLVING the SCHRODINGER EQUATION | Quantum Physics by …

What does the Hamiltonian operator represent?

In quantum mechanics, the Hamiltonian of a system is an operator corresponding to the total energy of that system, including both kinetic energy and potential energy.

Keywords People Search

• Which of the following wave function is the solution of Schrödinger equation?
• Hamiltonian (quantum mechanics) – Wikipedia

What is the physical significance of Sai square?

The square of the wave function, Ψ2, however, does have physical significance: the probability of finding the particle described by a specific wave function Ψ at a given point and time is proportional to the value of Ψ2. 11 thg 8, 2019

Keywords People Search

• What is the physical significance of wave function and ψ2?
• what is the physical significance of Ψ2 – Brainly.in

What is the physical significance of PSI square?

PSI represents the amplitude of the electron wave. It is commonly called wave function. It is a mathematical function and has no physical meaning by itself. Magnitude of psi square has the physical meaning as it determines the probability of density of finding the electron at that point. 26 thg 8, 2019

Keywords People Search

• What is the physical significance of wave function and ψ2?
• What is the significance of psi and psi square chemistry? – Brainly.in

show that the spherical harmonics are eigenfunctions of the operator – Spherical harmonics as Eigen functions of angular momentum

Watch The Video Below

Pictures on the topic show that the spherical harmonics are eigenfunctions of the operator | Spherical harmonics as Eigen functions of angular momentum

What is the significance of Ψ and ψ2 in quantum mechanical model of atom?

The wave function, ψ, is also called an atomic orbital. While the wave function, ψ, has no physical meaning, the square of the wave function, ψ2, is does. probability that the electron will be found at a particular location in an atom. particular location.

Keywords People Search

• What is the physical significance of wave function and ψ2?
• Chem 103, Section F0F Lecture 7 – The Quantum Mec

What is the expression for the Hamiltonian operator Mcq?

From the above, it is clear that if The energy operator for 1 particle in one dimension in quantum mechanics, H = − h 2 Δ 2 2 m + V ( r , t ) is called the Hamiltonian operator.

Keywords People Search

• What is the expression of Hamiltonian operator?
• Schrödinger’s Equation and the Hydrogen Atom MCQ [Free PDF]

What is Hamilton equation?

If the constraints in the problem do not depend explicitly on time, then it may be shown that H = T + V, where T is the kinetic energy and V is the potential energy of the system—i.e., the Hamiltonian is equal to the total energy of the system.

Keywords People Search

• What is the expression of Hamiltonian operator?
• mechanics – Lagrange’s and Hamilton’s equations | Britannica

What are the eigenstates and eigenvalues of the Hamiltonian?

When discussing the eigenstates of the Hamiltonian (ˆH), the associated eigenvalues represent energies and within the context of the momentum operators, the associated eigenvalues refer to the momentum of the particle. 8 thg 9, 2021

Keywords People Search

• What is the expression of Hamiltonian operator?
• 3.3: The Schrödinger Equation is an Eigenvalue Problem

What are the eigenvalues and eigenfunctions?

Such an equation, where the operator, operating on a function, produces a constant times the function, is called an eigenvalue equation. The function is called an eigenfunction, and the resulting numerical value is called the eigenvalue. Eigen here is the German word meaning self or own. 22 thg 7, 2021

Keywords People Search

• Are wave functions eigenfunctions?
• 3.4: Operators, Eigenfunctions, Eigenvalues, and Eigenstates

What are eigenfunctions and eigenvalues in chemistry?

When an operator operating on a function results in a constant times the function, the function is called an eigenfunction of the operator & the constant is called the eigenvalue. i.e. A f(x) = k f(x) where f(x) is the eigenfunction & k is the eigenvalue. 11 thg 10, 2011

Keywords People Search

• Are wave functions eigenfunctions?
• what is the eigen value and eigen function – Chemistry | 40j1tell

What do you mean by eigenfunctions and eigenvalues in physics?

In the case of Schrodinger’s equation, the eigenvalues are the possible energies that the system can have if it is in a state of well-defined energy. Each eigenfunction (of the Hamiltonian) is the state of the system when its energy is equal to the associated eigenvalue. 6 thg 12, 2018

Keywords People Search

• Are wave functions eigenfunctions?
• What is eigenvalue and eigenfunction in quantum mechanics?

Is Hamiltonian an observable?

The Hamiltonian is always an observable. 15 thg 11, 2020

Keywords People Search

• What kind of operator is the Hamiltonian?
• Is the Hamiltonian an Observable? – Physics Stack Exchange

Is the Hamiltonian a linear operator?

The Hamiltonian operator is often described as a linear operator because it has the linear property that H[Aψ(x)+Bϕ(x)]=AHψ(x)+BHϕ(x) H [ A ψ ( x ) + B ϕ ( x ) ] = A H ψ ( x ) + B H ϕ ( x ) for any two functions ψ(x) and ϕ(x) and any two constant numbers A and B .

Keywords People Search

• What kind of operator is the Hamiltonian?
• The Hamiltonian operator is often described as a linear … – Study.com

What are the operators?

In mathematics and sometimes in computer programming, an operator is a character that represents an action, as for example x is an arithmetic operator that represents multiplication. In computer programs, one of the most familiar sets of operators, the Boolean operators, is used to work with true/false values.

Keywords People Search

• What kind of operator is the Hamiltonian?
• What is operator? – Definition from WhatIs.com

What is Eigen value and eigen function in quantum mechanics?

An eigenfunction of an operator is a function such that the application of on gives. again, times a constant. (49) where k is a constant called the eigenvalue. It is easy to show that if is a linear operator with an eigenfunction , then any multiple of is also an eigenfunction of .

Keywords People Search

• What is the eigen value when the eigen function EX * is operated on the operator D DX?
• Eigenfunctions and Eigenvalues

How do you find the eigenvalue of an operator?

For a given linear operator T : V → V , a nonzero vector x and a constant scalar λ are called an eigenvector and its eigenvalue, respec- tively, when T(x) = λx. For a given eigenvalue λ, the set of all x such that T(x) = λx is called the λ-eigenspace.

Keywords People Search

• What is the eigen value when the eigen function EX * is operated on the operator D DX?
• Eigenvalues, eigenvectors, and eigenspaces of linear operators …

What is an operator in quantum mechanics?

An operator is a generalization of the concept of a function applied to a function. Whereas a function is a rule for turning one number into another, an operator is a rule for turning one function into another. 8 thg 9, 2021

Keywords People Search

• What is the eigen value when the eigen function EX * is operated on the operator D DX?
• 3.2: Linear Operators in Quantum Mechanics – Chemistry LibreTexts

Do commuting operators have common eigenfunctions?

18 Eigenfunctions of commuting operators. , have a common set of eigenfunctions, provided only that each has a complete set of eigenfunctions.

Keywords People Search

• When two operators commute What can we say about their eigenfunctions?
• D.18 Eigenfunctions of commuting operators

What are simultaneous eigenfunctions?

The simultaneous eigenfunctions of L2 and Lz are the spherical harmonics Ylm(θ, φ) and the simultaneous eigenfunctions of S2 and Sz are |SMs〉 with S = 1 and Ms = 1,0, − 1. From: Atoms and Molecules, 1978.

Keywords People Search

• When two operators commute What can we say about their eigenfunctions?
• Simultaneous Eigenfunctions – an overview | ScienceDirect Topics

What are simultaneous Eigen kets?

It means that you can write and , which means is the eigenket of both A and B, so their “simultaneous eigenket”! Reply. 12 thg 2, 2015

Keywords People Search

• When two operators commute What can we say about their eigenfunctions?
• Simultaneous Eigenkets? | Physics Forums

When two operators commute What can we say about their eigenfunctions?

If two operators commute and consequently have the same set of eigenfunctions, then the corresponding physical quantities can be evaluated or measured exactly simultaneously with no limit on the uncertainty. 18 thg 3, 2020

Keywords People Search

• What is a simultaneous Eigenket?
• 4.6: Commuting Operators Allow Infinite Precision

Do commuting operators have the same eigenvalues?

Commuting Operators Have the Same Eigenvectors, but not Eigenvalues. 28 thg 4, 2019

Keywords People Search

• What is a simultaneous Eigenket?
• Commuting Operators Have the Same Eigenvectors, but not Eigenvalues.

How do you show two operators commute?

Updating

Keywords People Search

• What is a simultaneous Eigenket?
• Quantum Mechanics | Commutation of Operators [Example #2] – YouTube

What operators commute with the Hamiltonian?

Now: Operators or observables that commute with the Hamiltonian of the system are conserved quantities, e.g. angular momentum or spin. This means that these quantities do not change with time. Those that do not commute with the Hamiltonian, are not conserved quantities. 21 thg 2, 2021

Keywords People Search

• How do you show two operators commute?
• What does “”commuting with the Hamiltonian”” mean?

What does it mean that two operators commute?

If two operators commute then both quantities can be measured at the same time, if not then there is a tradeoff in the accuracy in the measurement for one quantity vs. the other. 15 thg 8, 2020

Keywords People Search

• How do you show two operators commute?
• Commuting Operators – Chemistry LibreTexts

What is commute and anti commute?

Anticommutative means the product in one order is the negation of the product in the other order, that is, when . (Noncommutative is a weaker statement. It says .) This comes up for a matrix representation for the quaternions in the real matrix ring .

Keywords People Search

• How do you show two operators commute?
• When are two matrices said to be anti-commutative? – Quora

What is angular momentum vector in an orbital motion?

Angular momentum is a vector quantity whose direction is perpendicular to plane of revolution.

Keywords People Search

• What is ordinary angular momentum?
• In an orbital motion, the angular momentum vector is – Toppr

How do you find angular momentum?

Linear momentum (p) is defined as the mass (m) of an object multiplied by the velocity (v) of that object: p = m*v. With a bit of a simplification, angular momentum (L) is defined as the distance of the object from a rotation axis multiplied by the linear momentum: L = r*p or L = mvr.

Keywords People Search

• What is ordinary angular momentum?
• Astronomy 201: Angular Momentum

Why is angular momentum important in astronomy?

The concept of angular momentum is important in physics because it is a conserved quantity: a system’s angular momentum stays constant unless an external torque acts on it. Torque is the rate at which angular momentum is transferred in or out of the system.

Keywords People Search

• What is ordinary angular momentum?
• Angular momentum – New World Encyclopedia

What is angular momentum example?

Another popular example of the conservation of angular momentum is that of a person holding a spinning bicycle wheel on a rotating chair. The person then turns over the bicycle wheel, causing it to rotate in an opposite direction, as shown below.

Keywords People Search

• How do you find the orbital angular momentum?
• Conservation of Angular Momentum | SparkNotes

Do orbitals have angular momentum?

Orbital angular momentum is a property of the electron’s rotational motion that is related to the shape of its orbital. The orbital is the region around the nucleus where the electron will be found if detection is undertaken. 20 thg 4, 2017

Keywords People Search

• How do you find the orbital angular momentum?
• orbital angular momentum – Quantum Physics Lady

Which of the following angular momentum shows presence of electrons in orbit?

Correct option is “”d””. Note: nh/2π gives angular momentum of electron revolving in a circular orbit as proposed by Neils Bohr.

Keywords People Search

• How do you find the orbital angular momentum?
• orbital angular momentum Formula | IIT JEE NEET solved problems

What is known as angular momentum operator?

In quantum mechanics, the angular momentum operator is one of several related operators analogous to classical angular momentum. The angular momentum operator plays a central role in the theory of atomic and molecular physics and other quantum problems involving rotational symmetry.

Keywords People Search

• What is generalized angular momentum?
• Angular momentum operator – Wikipedia

What is total angular momentum operator?

In quantum mechanics, angular momentum is a vector operator of which the three components have well-defined commutation relations. This operator is the quantum analogue of the classical angular momentum vector. 15 thg 12, 2010

Keywords People Search

• What is generalized angular momentum?
• Angular momentum (quantum) – Knowino

Does angular momentum commute with Hamiltonian?

Angular momentum operator L commutes with the total energy Hamiltonian operator (H).

Keywords People Search

• What is generalized angular momentum?
• Angular Momentum and Central Forces

Are spherical harmonics eigenfunctions of angular momentum?

The spherical harmonics play an important role in quantum mechanics. They are eigenfunctions of the operator of orbital angular momentum and describe the angular distribution of particles which move in a spherically-symmetric field with the orbital angular momentum l and projection m.

Keywords People Search

• What is the eigenfunction of the orbital angular momentum operator?
• SPHERICAL HARMONICS | Quantum Theory of Angular Momentum

Is the function an eigenfunction of the operator?

Such an equation is called an eigenvalue equation. The function eax is an eigenfunction of the operator d/dx because (d/dx)eax ¼ aeax, which is a constant (a) multiplying the original function.

Keywords People Search

• What is the eigenfunction of the orbital angular momentum operator?
• The foundations of quantum mechanics

What is the difference between orbital angular momentum and spin angular momentum?

Definition in classical mechanics. Just as for angular velocity, there are two special types of angular momentum of an object: the spin angular momentum is the angular momentum about the object’s centre of mass, while the orbital angular momentum is the angular momentum about a chosen center of rotation.

Keywords People Search

• What is the eigenfunction of the orbital angular momentum operator?
• Angular momentum – Wikipedia

How do you find eigenvalues of angular momentum operator?

Updating

Keywords People Search

• What is the eigen function of angular momentum?
• Angular momentum eigenvalues – YouTube

What is the eigenvalue for the z component of the angular momentum?

Traditionally, ml is defined to be the z component of the angular momentum l , and it is the eigenvalue (the quantity we expect to see over and over again), in units of ℏ , of the wave function, ψ . 21 thg 12, 2016

Keywords People Search

• What is the eigen function of angular momentum?
• What Is Z component of orbital angular momentum? How can we find the …

What are the dimensions of angular momentum?

M1 L2 T – 1 Therefore, the angular momentum is dimensionally represented as M1 L2 T – 1. 2 thg 8, 2019

Keywords People Search

• What is the eigen function of angular momentum?
• Dimensional Formula of Angular Momentum and its Derivation – Byjus

How do you find eigenvalues and eigenfunctions of an operator?

Updating

Keywords People Search

• How do you find eigenvalues in quantum mechanics?
• Quantum Chemistry 3.3 – Eigenvalues and Eigenfunctions – YouTube

How do you find the eigenvalues of a Hamiltonian matrix?

To find the eigenvalues E we set the determinant of the matrix (H – EI) equal to zero and solve for E. To find the corresponding eigenvectors {|Ψ>}, we substitute each eigenvalue E back into the equation (H-E*I)|Ψ> = 0 and solve for the expansion coefficients of |Ψ> in the given basis.

Keywords People Search

• How do you find eigenvalues in quantum mechanics?
• Eigenvalues

What are the eigenstates of the Hamiltonian?

A system prepared in an eigenstate of the Hamiltonian has time-invariant probability density. A system prepared in an eigenstate of a non-commuting operator has a probability density which varies in time. It is this time independence (conservation law) which makes eigenstates of the energy operator so useful.

Keywords People Search

• How do you find eigenvalues in quantum mechanics?
• 1 Summary of things you should already know

Which of the following are eigenfunctions of the momentum operator?

Ψ(x) is the eigenfunction of the momentum operator with the eigenvalue λ = − ℏ k \lambda = -\hbar k λ=−ℏk. 4 thg 6, 2021

Keywords People Search

• What is meant by eigenfunctions and eigenvalues?
• Answer to Question #203210 in Physics for Vinod Kumar

What do you mean by eigenfunctions?

In mathematics, an eigenfunction of a linear operator D defined on some function space is any non-zero function in that space that, when acted upon by D, is only multiplied by some scaling factor called an eigenvalue.

Keywords People Search

• What is meant by eigenfunctions and eigenvalues?
• Eigenfunction – Wikipedia

Which of the following functions are eigenfunctions of the operator D DX?

Which of the following is Eigen function of D DX? The function eax is aneigenfunction of the operator d/dx because (d/dx)eax ¼ aeax, which is a constant (a) multiplying the original function. … The constant o in an eigenvalueequation is called theeigenvalue of the operator O. 22 thg 12, 2020

Keywords People Search

• What is meant by eigenfunctions and eigenvalues?
• which of the following functions are eigen functions of d2/dx2. 1). Sin3x.

What is Hamiltonian operator in chemistry?

The Hamiltonian operator is the sum of the kinetic energy operator and potential energy operator. The kinetic energy operator is the same for all models but the potential energy changes and is the defining parameter. 22 thg 5, 2020

Keywords People Search

• What are eigenfunctions and eigenvalues in chemistry?
• Quantum Mechanical H Atom – Chemistry LibreTexts

How do you show eigenfunctions are orthogonal?

Multiply the first equation by φ∗ and the second by ψ and integrate. If a1 and a2 in Equation 4.5. 14 are not equal, then the integral must be zero. This result proves that nondegenerate eigenfunctions of the same operator are orthogonal. 18 thg 3, 2020

Keywords People Search

• What do you mean by eigenfunctions and eigenvalues in physics?
• 4.5: Eigenfunctions of Operators are Orthogonal – Chemistry LibreTexts

What are the eigenstates and eigenvalues of the Hamiltonian?

When discussing the eigenstates of the Hamiltonian (ˆH), the associated eigenvalues represent energies and within the context of the momentum operators, the associated eigenvalues refer to the momentum of the particle. 8 thg 9, 2021

Keywords People Search

• Which of the following are eigenfunctions for the operator d2 dx2?
• 3.3: The Schrödinger Equation is an Eigenvalue Problem

show that the spherical harmonics are eigenfunctions of the operator – 18 7 Spherical Harmonic Eigenfunctions

Watch Video Now

Pictures on the topic show that the spherical harmonics are eigenfunctions of the operator | 18 7 Spherical Harmonic Eigenfunctions

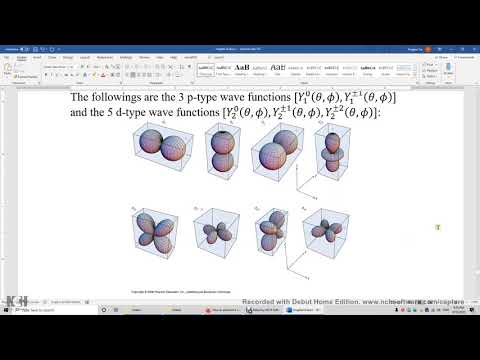
Is D DX a linear operator?

However d/dx is considered to be a linear operator. If I understand this correctly, that means we have to convert the function we are taking the derivative of into a vector that represents it. The linear operator then maps the vector to another vector which represents a new polynomial. 9 thg 8, 2019

Keywords People Search

• Which of the following are eigenfunctions for the operator d2 dx2?
• The Derivative of a Linear Operator – calculus – Math Stack Exchange

What is the eigenvalue of the function e ax when operated with d’n DX N?

Explanation: a^ne^x is the eigen value of the function e^ax when operated on the operator d^n/dx^n. 19 thg 10, 2020

Keywords People Search

• Which of the following are eigenfunctions for the operator d2 dx2?
• What is the eigen value of the function e^ax when operated – Brainly.in

Is D DX Hermitian operator?

Conclusion: d/dx is not Hermitian. Its Hermitian conju- gate is −d/dx.

Keywords People Search

• Is K an eigenfunction of D DX?
• OPERATORS An operator is a recipe showing how to get a function g …

Is Multiplication a linear operator?

The linear operator of multiplication by a sequence (respectively, a function) in (respectively, in ) is self-adjoint if and only if this sequence (function) is real valued. A linear integral operator is self-adjoint if and only if almost-everywhere. In shift operators and the Fourier operator are unitary. 29 thg 10, 2017

Keywords People Search

• Is K an eigenfunction of D DX?
• Linear operator – Encyclopedia of Mathematics

What is the potential V for a free particle?

In quantum mechanics, it means the particle is in a region of uniform potential, usually set to zero in the region of interest since the potential can be arbitrarily set to zero at any point in space.

Keywords People Search

• Is K an eigenfunction of D DX?
• Free particle – Wikipedia

What are the types of operator?

There are three types of operator that programmers use: arithmetic operators. relational operators. logical operators.

Keywords People Search

• What are the operators?
• Operators – Data types and structures – GCSE Computer Science Revision

What is an example of an operator?

The definition of an operator is someone who controls a machine, or the manager or owner of a business. An example of an operator is a person who controls a telephone switchboard. An example of an operator is someone who controls a crane at a loading dock.

Keywords People Search

• What are the operators?
• Operator Meaning | Best 27 Definitions of Operator

What is an operator explain different types of operators?

Operators can be defined as basic symbols that help us work on logical and mathematical operations. Operators in C and C++, are tools or symbols that are used to perform mathematical operations concerning arithmetic, logical, conditional and, bitwise operations. 21 thg 8, 2019

Keywords People Search

• What are the operators?
• 6 Types of Operators in C and C++ | Enhance Your Fundamental Skills …

How do you find eigenstates of an operator?

Updating

Keywords People Search

• What are the eigenstates of the Hamiltonian?
• Eigenvalues and eigenstates in quantum mechanics – YouTube

Are eigenvectors and Eigenstates the same?

is that eigenvector is (linear algebra) a vector that is not rotated under a given linear transformation; a left or right eigenvector depending on context while eigenstate is (physics) a dynamic quantum mechanical state whose wave function is an eigenvector that corresponds to a physical quantity.

Keywords People Search

• What are the eigenstates of the Hamiltonian?
• Eigenvector vs Eigenstate – What’s the difference? | WikiDiff

What is meant by energy eigenstates?

An eigenstate is a possible state of the system when it has a definite value of some parameter. E.g. momentum or position or energy. If it is an energy eigenstate then the system has an amount of energy. More eigenstates represent more possibilities for the system, so they don’t mean more energy.

Keywords People Search

• What are the eigenstates of the Hamiltonian?
• What are eigenstates? Do they have energy, and do more … – Quora

What are eigenvalues and eigenfunctions?

Such an equation, where the operator, operating on a function, produces a constant times the function, is called an eigenvalue equation. The function is called an eigenfunction, and the resulting numerical value is called the eigenvalue. 22 thg 7, 2021

Keywords People Search

• Are eigenvectors and Eigenstates the same?
• 3.4: Operators, Eigenfunctions, Eigenvalues, and Eigenstates

How do you find the eigenvectors of an operator?

For a given linear operator T : V → V , a nonzero vector x and a constant scalar λ are called an eigenvector and its eigenvalue, respec- tively, when T(x) = λx. For a given eigenvalue λ, the set of all x such that T(x) = λx is called the λ-eigenspace.

Keywords People Search

• Are eigenvectors and Eigenstates the same?
• Eigenvalues, eigenvectors, and eigenspaces of linear operators …

What are eigenvalues and eigenstates?

These special wavefunctions are called eigenstates, and the multiples are called eigenvalues. Thus, if Aψa(x)=aψa(x), where a is a complex number, then ψa is called an eigenstate of A corresponding to the eigenvalue a. 11 thg 8, 2020

Keywords People Search

• Are eigenvectors and Eigenstates the same?
• 3.8: Eigenstates and Eigenvalues – Physics LibreTexts

What is Eigenstates in quantum mechanics?

An eigenstate is a quantum state whose wave function is an eigenfunction of the linear operator that corresponds with an observable. The eigenvalue of that wave function would be the quantity you observe when you measure that observable (the eigenvalue could be a vector quantity).

Keywords People Search

• What are Eigenstates?
• Quantum Mechanics: What is an eigenstate? – Quora

What are quantum Eigenstates?

An eigenstate is the measured state of some object possessing quantifiable characteristics such as position, momentum, etc.

Keywords People Search

• What are Eigenstates?
• Introduction to eigenstates – Wikipedia

Are all Eigenstates orthogonal?

Originally Answered: Are all eigen Vectors Orthonormal? No, unless you choose them to be. However, if you have an orthogonal basis of eigenvectors, it is easy to convert it into an orthonormal basis.

Keywords People Search

• What are Eigenstates?
• Are all eigenvectors orthonormal? – Quora

Are spherical harmonics eigenfunctions?

Spherical harmonics are defined as the eigenfunctions of the angular part of the Laplacian in three dimensions. As a result, they are extremely convenient in representing solutions to partial differential equations in which the Laplacian appears.

Keywords People Search

• What are spherical harmonic functions?
• Spherical Harmonics | Brilliant Math & Science Wiki

Where are spherical harmonics used?

Spherical harmonics are important in many theoretical and practical applications, including the representation of multipole electrostatic and electromagnetic fields, electron configurations, gravitational fields, geoids, the magnetic fields of planetary bodies and stars, and the cosmic microwave background radiation.

Keywords People Search

• What are spherical harmonic functions?
• Spherical harmonics – Wikipedia

What are spherical harmonic coefficients?

The spherical harmonics are the angular portion of the solution to Laplace’s equation in spherical coordinates where azimuthal symmetry is not present.

Keywords People Search

• What are spherical harmonic functions?
• Spherical Harmonic — from Wolfram MathWorld

How do you find spherical harmonics?

ℓ (θ, φ) = ℓ(ℓ + 1)Y m ℓ (θ, φ) . That is, the spherical harmonics are eigenfunctions of the differential operator L2, with corresponding eigenvalues ℓ(ℓ + 1), for ℓ = 0, 1, 2, 3,….

Keywords People Search

• Where are spherical harmonics used?
• The Spherical Harmonics

What is spherical harmonics in chemistry?

Spherical Harmonics are a group of functions used in math and the physical sciences to solve problems in disciplines including geometry, partial differential equations, and group theory. The general, normalized Spherical Harmonic is depicted below: Yml(θ,ϕ)=√(2l+1)(l−|m|)! 14 thg 11, 2020

Keywords People Search

• Where are spherical harmonics used?
• Spherical Harmonics – Chemistry LibreTexts

Are spherical harmonics symmetric?

The spherical harmonics are often represented graphically since their linear combinations correspond to the angular functions of orbitals. Figure 1.1a shows a plot of the spherical harmonics where the phase is color coded. One can clearly see that is symmetric for a rotation about the z axis.

Keywords People Search

• Where are spherical harmonics used?
• 1 Properties of Spherical Harmonics

What is a spherical harmonic degree?

Spherical harmonics are the spherical analogue of trigonometric polynomials on [−π,π). The degree ℓ≥0, order m (−ℓ≤m≤m) spherical harmonic is denoted by Ymℓ(λ,θ), and can be expressed (in real form) as [1, Sec.

Keywords People Search

• What are spherical harmonic coefficients?
• Spherical harmonics – Chebfun

Are spherical harmonics real?

Real spherical harmonics (RSH) are obtained by combining complex conjugate functions associated to opposite values of . RSH are the most adequate basis functions for calculations in which atomic symmetry is important since they can be directly related to the irreducible representations of the subgroups of [Blanco1997].

Keywords People Search

• What are spherical harmonic coefficients?
• Complex and Real Spherical Harmonics – abinit

What does it mean for a function to be harmonic?

harmonic function, mathematical function of two variables having the property that its value at any point is equal to the average of its values along any circle around that point, provided the function is defined within the circle.

Keywords People Search

• How do you find spherical harmonics?
• harmonic function | mathematics – Encyclopedia Britannica

What is meant by zonal harmonics?

A zonal harmonic is a spherical harmonic of the form , i.e., one which reduces to a Legendre polynomial (Whittaker and Watson 1990, p. 302). These harmonics are termed “zonal” since the curves on a unit sphere (with center at the origin) on which vanishes are.

Keywords People Search

• What is spherical harmonics in chemistry?
• Zonal Harmonic — from Wolfram MathWorld

What is the orbital angular momentum?

What is orbital angular momentum? A property of an electron’s rotational motion which is related to the shape of its orbital is the Orbital Angular Momentum. The orbital is known as the region that is around the nucleus where the electron will be found if detection is undertaken.

Keywords People Search

• What is spherical harmonics in chemistry?
• Orbital Angular Momentum – Example, Explanation, Applications

Are spherical harmonics eigenfunctions of angular momentum?

The spherical harmonics play an important role in quantum mechanics. They are eigenfunctions of the operator of orbital angular momentum and describe the angular distribution of particles which move in a spherically-symmetric field with the orbital angular momentum l and projection m.

Keywords People Search

• What is spherical harmonics in quantum mechanics?
• SPHERICAL HARMONICS | Quantum Theory of Angular Momentum

How do you decompose a function into spherical harmonics?

If you have a function f(x), you can decompose it as an infinite sum of sine waves of the form sin(nx) and cos(nx) for increasing n. If you have a function g(theta,phi), you can decompose it into spherical harmonics; for each order l you have 2l+1 spherical harmonics. 26 thg 9, 2007

Keywords People Search

• What is spherical harmonics in quantum mechanics?
• Spherical harmonic decomposition | Physics Forums

What does orthonormal mean in linear algebra?

In linear algebra, two vectors in an inner product space are orthonormal if they are orthogonal (or perpendicular along a line) unit vectors. A set of vectors form an orthonormal set if all vectors in the set are mutually orthogonal and all of unit length.

Keywords People Search

• Are spherical harmonics Orthonormal?
• Orthonormality – Wikipedia

How do you find the harmonic conjugate?

Updating

Keywords People Search

• How do you show a harmonic function?
• How to Find a Harmonic Conjugate for a Complex Valued Function

What are harmonics math?

In mathematics, the harmonic series is the infinite series formed by summing all positive unit fractions: The first terms of the series sum to approximately , where is the natural logarithm and.

Keywords People Search

• How do you show a harmonic function?
• Harmonic series (mathematics) – Wikipedia

What makes an equation harmonic?

A real-valued function is considered harmonic in a domain D if all of its second-order partial derivatives are continuous in D, and if at each point in D the function satisfies Laplace’s equation [1]. Such functions come from the real and imaginary parts of complex analytical functions.

Keywords People Search

• How do you show a harmonic function?
• Harmonic Equations

How do you show a harmonic function?

If f(z) = u(x, y) + iv(x, y) is analytic on a region A then both u and v are harmonic functions on A. Proof. This is a simple consequence of the Cauchy-Riemann equations.

Keywords People Search

• Why are harmonic functions called harmonic?
• Topic 5 Notes 5 Introduction to harmonic functions

What do you mean by the harmonic conjugate?

Definition of harmonic conjugates : the two points that divide a line segment internally and externally in the same ratio.

Keywords People Search

• Why are harmonic functions called harmonic?
• Harmonic conjugates Definition & Meaning – Merriam-Webster

What is a harmonic function in physics?

In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R, where U is an open subset of Rn, that satisfies Laplace’s equation, that is, everywhere on U.

Keywords People Search

• Why are harmonic functions called harmonic?
• Harmonic function – Wikipedia

What is a sphere in math?

sphere, In geometry, the set of all points in three-dimensional space lying the same distance (the radius) from a given point (the centre), or the result of rotating a circle about one of its diameters.

Keywords People Search

• Are spherical harmonics complex?
• sphere | mathematics – Encyclopedia Britannica

What is harmonic conjugate in complex analysis?

In Complex Analysis, Harmonic Conjugate are those which satisfy both Cauchy–Riemann equations & Laplace’s equation . The Cauchy–Riemann equations on a pair of real-valued functions of two real variables u(x,y) and v(x,y) are the two equations: Now, Thus, which is the Laplace Equation.

Keywords People Search

• What does it mean for a function to be harmonic?
• What is harmonic conjugate? – Quora

What is harmonic function in physics class 11?

Any real function with continuous second partial derivatives which satisfies Lallace’s equation. is called a harmonic function. 14 thg 1, 2014

Keywords People Search

• What does it mean for a function to be harmonic?
• what is a harmonic function – Physics – TopperLearning.com | r8697oll

Does harmonic imply holomorphic?

The Cauchy-Riemann equations for a holomorphic function imply quickly that the real and imaginary parts of a holomorphic function are harmonic.

Keywords People Search

• What does it mean for a function to be harmonic?
• PDF – 18.112 Functions of a Complex Variable

Which of the following are eigenfunctions of the momentum operator?

Ψ(x) is the eigenfunction of the momentum operator with the eigenvalue λ = − ℏ k \lambda = -\hbar k λ=−ℏk. 4 thg 6, 2021

Keywords People Search

• How do you find eigenvalues and eigenfunctions of an operator?
• Answer to Question #203210 in Physics for Vinod Kumar

How do you calculate eigenfunctions?

Updating

Keywords People Search

• How do you find eigenvalues and eigenfunctions of an operator?
• Eigenfunctions and Eigenvalues – YouTube

Which of the following functions are eigenfunctions of the operator D DX?

Which of the following is Eigen function of D DX? The function eax is aneigenfunction of the operator d/dx because (d/dx)eax ¼ aeax, which is a constant (a) multiplying the original function. … The constant o in an eigenvalueequation is called theeigenvalue of the operator O. 22 thg 12, 2020

Keywords People Search

• How do you find eigenvalues and eigenfunctions of an operator?
• which of the following functions are eigen functions of d2/dx2. 1). Sin3x.

What are the eigenstates and eigenvalues of the Hamiltonian?

When discussing the eigenstates of the Hamiltonian (ˆH), the associated eigenvalues represent energies and within the context of the momentum operators, the associated eigenvalues refer to the momentum of the particle. 8 thg 9, 2021

Keywords People Search

• How do you find the eigenvalues of a Hamiltonian matrix?
• 3.3: The Schrödinger Equation is an Eigenvalue Problem

How do you find the eigenvalues of a Hermitian operator?

PROVE: The eigenvalues of a Hermitian operator are real. (This means they represent a physical quantity.) *Aφi dτ = ∫ φi (Aφi)* dτ.

Keywords People Search

• How do you find the eigenvalues of a Hamiltonian matrix?
• theorems of quantum mechanics

What are the eigenvectors of a Hamiltonian?

In the case of Hamiltonian, eigenvectors are states with definite energy. Now, quantum states evolves by the factor from the Schrodinger’s equation. So a state with definite energy evolves by only multiplying a phase factor in front, i.e. A state with definite energy remains a state with definite energy. 31 thg 8, 2011

Keywords People Search

• How do you find the eigenvalues of a Hamiltonian matrix?
• Eigenvectors of the Hamiltonian | Physics Forums

What are the eigenfunctions and eigenvalues of the momentum operator?

If the momentum operator operates on a wave function and IF AND ONLY IF the result of that operation is a constant multiplied by the wave function, then that wave function is an eigenfunction or eigenstate of the momentum operator, and its eigenvalue is the momentum of the particle.

Keywords People Search

• Which of the following are eigenfunctions of the momentum operator?
• basics of quantum mechanics – Oregon State University

What is the momentum for a particle trapped in a box?

3.7: The Average Momentum of a Particle in a Box is Zero – Chemistry LibreTexts. 18 thg 3, 2020

Keywords People Search

• Which of the following are eigenfunctions of the momentum operator?
• 3.7: The Average Momentum of a Particle in a Box is Zero

What are momentum eigenstates?

The momentum eigenstates have a continuous range of eigenvalues so that they cannot be indexed like the energy eigenstates of a bound system. This means the Kronecker delta could not work anyway. These are the momentum eigenstates.

Keywords People Search

• Which of the following are eigenfunctions of the momentum operator?
• Momentum Eigenfunctions

How do you find the momentum operator?

Updating

Keywords People Search

• What is momentum operator squared?
• Momentum operator, energy operator, and a differential equation – YouTube

What is linear momentum operator?

The Linear Momentum Operator is the quantum mechanical operator which gives an instruction to differentiate with respect to x (position) and multiply by −iℏ.

Keywords People Search

• What is momentum operator squared?
• Linear Momentum Operator | Quatomic

Which operator is associated with momentum?

The Hamiltonian Operator Name Observable Symbol Operator Symbol Momentum (in 3D) →p ˆP Kinetic Energy (in 1D) Tx ^Tx Kinetic Energy (in 3D) T ˆT Potential Energy (in 1D) V(x) ˆV(x) 8 hàng khác • 8 thg 9, 2021

Keywords People Search

• What is momentum operator squared?
• 4.2: Quantum Operators Represent Classical Variables

What is the expectation value of the momentum of the particle?

While the expectation value of a function of position has the appearance of an average of the function, the expectation value of momentum involves the representation of momentum as a quantum mechanical operator. is the operator for the x component of momentum. for a particle in one dimension.

Keywords People Search

• What is the expectation value of momentum of a particle trapped in a one dimensional box?
• Expectation Values in Quantum Mechanics – HyperPhysics

What is momentum operator quantum mechanics?

In quantum mechanics, the momentum operator is the operator associated with the linear momentum. The momentum operator is, in the position representation, an example of a differential operator.

Keywords People Search

• What is the expectation value of momentum of a particle trapped in a one dimensional box?
• Momentum operator – Wikipedia

How do you calculate the expectation value of a Hamiltonian?

The Hamiltonian is ˆH(x,ℏ∂22m∂x2). To get an expectation value I need to integrate this: ∫ψ∗ˆHψdx. 21 thg 4, 2014

Keywords People Search

• What is the expectation value of momentum of a particle trapped in a one dimensional box?
• Calculating the expectation value of a Hamiltonian – Physics Stack …

Why is tunneling used in quantum mechanics?

Tunneling is a quantum mechanical phenomenon when a particle is able to penetrate through a potential energy barrier that is higher in energy than the particle’s kinetic energy. This amazing property of microscopic particles play important roles in explaining several physical phenomena including radioactive decay. 27 thg 4, 2016

Keywords People Search

• What is meant by quantum tunneling?
• 4.9: Quantum-Mechanical Tunneling – Chemistry LibreTexts

Do transistors use quantum tunneling?

On the other hand, a Bizen transistor uses quantum-tunnel technology, which eliminates the resistor (as with MOS devices) and allows designers to take advantage of the now-controllable current. 16 thg 6, 2020

Keywords People Search

• What is meant by quantum tunneling?
• Are Quantum-Tunnel Transistors Real, and What Do They Mean for …

What is tunneling service?

Tunneling is the process by which VPN packets reach their intended destination, which is typically a private network. Many VPNs use the IPsec protocol suite. IPsec is a group of protocols that run directly on top of IP at the network layer.

Keywords People Search

• What is meant by quantum tunneling?
• What is tunneling? | Tunneling in networking | Cloudflare

What is linear operator?

a mathematical operator with the property that applying it to a linear combination of two objects yields the same linear combination as the result of applying it to the objects separately.

Keywords People Search

• What is linear momentum operator?
• Linear operator Definition & Meaning | Dictionary.com

What are eigenfunctions and eigenvalues?

An eigenfunction of an operator is a function such that the application of on gives. again, times a constant. (49) where k is a constant called the eigenvalue. It is easy to show that if is a linear operator with an eigenfunction , then any multiple of is also an eigenfunction of .

Keywords People Search

• What is linear momentum operator?
• Eigenfunctions and Eigenvalues

How do you use linear momentum operator?

Updating

Keywords People Search

• What is linear momentum operator?
• Kinetic energy and linear momentum operator derivations – YouTube

Which operator is Hamiltonian operator?

For every observable property of a system there is a corresponding quantum mechanical operator. The total energy operator is called the Hamiltonian operator, ˆH and consists of the kinetic energy operator plus the potential energy operator. 18 thg 3, 2020

Keywords People Search

• Which operator is associated with momentum?
• 4.2: Quantum Operators Represent Classical Variables

What does the Hamiltonian operator represents?

The Hamiltonian operator, H ^ ψ = E ψ , extracts eigenvalue E from eigenfunction ψ, in which ψ represents the state of a system and E its energy. The expression H ^ ψ = E ψ is Schrödinger’s time-independent equation.

Keywords People Search

• Which operator is associated with momentum?
• Hamiltonian Operator – an overview | ScienceDirect Topics

What is Hamiltonian operator in chemistry?

The Hamiltonian operator is the sum of the kinetic energy operator and potential energy operator. The kinetic energy operator is the same for all models but the potential energy changes and is the defining parameter. 22 thg 5, 2020

Keywords People Search

• Which operator is associated with momentum?
• Quantum Mechanical H Atom – Chemistry LibreTexts

How do you show eigenfunctions are orthogonal?

Multiply the first equation by φ∗ and the second by ψ and integrate. If a1 and a2 in Equation 4.5. 14 are not equal, then the integral must be zero. This result proves that nondegenerate eigenfunctions of the same operator are orthogonal. 18 thg 3, 2020

Keywords People Search

• What do you mean by eigenfunctions?
• 4.5: Eigenfunctions of Operators are Orthogonal – Chemistry LibreTexts

Which of the following wave functions are eigenfunctions of the operator d2 dx2?

cos(3x) is an eigenfunction of the operator d2/dx2.

Keywords People Search

• What do you mean by eigenfunctions?
• The foundations of quantum mechanics

Are all eigenfunctions orthogonal?

Eigenfunctions of a Hermitian operator are orthogonal if they have different eigenvalues. Because of this theorem, we can identify orthogonal functions easily without having to integrate or conduct an analysis based on symmetry or other considerations. 22 thg 10, 2021

Keywords People Search

• How do you show eigenfunctions are orthogonal?
• 4.5: Eigenfunctions of Operators are Orthogonal – Chemistry LibreTexts

What orthogonality condition do the eigenfunctions satisfy?

4. Orthogonality of Eigenfunctions Theorem: Eigenfunctions corresponding to distinct eigenvalues must be orthogonal. Xn(x)Xm(x)dx = 0.

Keywords People Search

• How do you show eigenfunctions are orthogonal?
• 3.8 (supplement) — orthogonality of eigenfunctions – Math

Do Hermitian operators have real eigenfunctions?

Hermitian operators have only real eigenvalues. Hermitian operators have a complete set of orthonormal eigenfunctions (or eigenvectors).

Keywords People Search

• How do you show eigenfunctions are orthogonal?
• 2.6 Hermitian Operators

Is K an eigenfunction of D DX?

How many different eigenfunctions are there for the operator d/dx? Since there are no restrictions on k, there are an infinite number of eigenfunctions of d/dx of this form.

Keywords People Search

• Which of the following functions are eigenfunctions of the operator D DX?
• notes_Ch3.pdf

What is the eigenvalue of e ax when operated on the operator DN DX?

Explanation: a^ne^x is the eigen value of the function e^ax when operated on the operator d^n/dx^n. 19 thg 10, 2020

Keywords People Search

• Which of the following functions are eigenfunctions of the operator D DX?
• What is the eigen value of the function e^ax when operated on … – Brainly.in

What are the operators?

In mathematics and sometimes in computer programming, an operator is a character that represents an action, as for example x is an arithmetic operator that represents multiplication. In computer programs, one of the most familiar sets of operators, the Boolean operators, is used to work with true/false values.

Keywords People Search

• Which of the following functions are eigenfunctions of the operator D DX?
• What is operator? – Definition from WhatIs.com

What is Sturm-Liouville eigenvalue problem?

The problem of finding a complex number µ if any, such that the BVP (6.2)-(6.3) with λ = µ, has a non-trivial solution is called a Sturm-Liouville Eigen Value Problem (SL-EVP). Such a value µ is called an eigenvalue and the corresponding non-trivial solutions y(.; µ) are called eigenfunctions.

Keywords People Search

• How are the eigenfunctions and eigenvalues related to the Sturm-Liouville problem?
• Chapter 6 Sturm-Liouville Problems – IITB Math

What makes a Sturm-Liouville problem?

(In the case of more general p(x), q(x), w(x), the solutions must be understood in a weak sense.) In addition, y is typically required to satisfy some boundary conditions at a and b. Each such equation (1) together with its boundary conditions constitutes a Sturm–Liouville (S-L) problem.

Keywords People Search

• How are the eigenfunctions and eigenvalues related to the Sturm-Liouville problem?
• Sturm–Liouville theory – Wikipedia

How do you identify a Sturm-Liouville problem?

Updating

Keywords People Search

• How are the eigenfunctions and eigenvalues related to the Sturm-Liouville problem?
• Sturm-Liouville Theorem and Proof – YouTube

How are the eigenfunctions and eigenvalues related to the Sturm-Liouville problem?

(p(x)y′)′ + (q(x) + λr(x))y = 0, a < x < b, (plus boundary conditions), is called an eigenfunction, and the corresponding value of λ is called its eigenvalue. The eigenvalues of a Sturm-Liouville problem are the values of λ for which nonzero solutions exist. 10 thg 4, 2012

Keywords People Search

• What makes a Sturm-Liouville problem?
• Introduction to Sturm-Liouville Theory – Trinity University

What is the eigenvalue problem?

The eigenvalue problem (EVP) consists of the minimization of the maximum eigenvalue of an n × n matrix A(P) that depends affinely on a variable, subject to LMI (symmetric) constraint B(P) > 0, i.e.,(11.58)λmax(A(P))→minP=PTB(P)>0.

Keywords People Search

• What makes a Sturm-Liouville problem?
• Eigenvalue Problems – an overview | ScienceDirect Topics

What is the Sturm-Liouville system?

Sturm-Liouville systems are second-order linear differential equations with boundary conditions of a particular type, and they usually arise from separation of variables in partial differential equations which represent physical systems. As an illustration we analyse small planar oscillations of hanging chain.

Keywords People Search

• What makes a Sturm-Liouville problem?
• Regular Sturm-Liouville Systems Shan Gao 250539905 1 …

How Fourier series solve differential equations explain in detail?

Updating

Keywords People Search

• How do you solve the strum Louville problem?
• Fourier series | Lecture 49 | Differential Equations for Engineers

How do you write equations in Sturm-Liouville?

Updating

Keywords People Search

• How do you solve the strum Louville problem?
• Putting an Equation in Sturm Liouville Form – YouTube

Are all operators linear?

The most basic operators (in some sense) are linear maps, which act on vector spaces. However, when using “linear operator” instead of “linear map”, mathematicians often mean actions on vector spaces of functions, which also preserve other properties, such as continuity.

Keywords People Search

• Is √ a linear operator?
• Operator (mathematics) – Wikipedia

Is the square root a linear operator?

Condition B does not hold, therefore the square root operator is not linear. The most operators encountered in quantum mechanics are linear operators. 5 thg 12, 2019

Keywords People Search

• Is √ a linear operator?
• 3.2: Linear Operators in Quantum Mechanics – Chemistry LibreTexts

How do you find the linear operator?

Updating

Keywords People Search

• Is √ a linear operator?
• Linear Operators Part 1 – YouTube

What is a linear operator matrix?

The matrix of a linear operator is square Remember that every linear map between two finite-dimensional vector spaces can be represented by a matrix , called the matrix of the linear map. The notation indicates that the matrix depends on the choice of two bases: a basis for the space and a basis for the space .

Keywords People Search

• How do you show an operator is linear?
• Linear operator – StatLect

What is a linear differential operator?

The differential operator is linear, that is, for all sufficiently differentiable functions and and all scalars . The proof is left as an exercise.

Keywords People Search

• How do you show an operator is linear?
• Linear Differential Operators – Ximera – The Ohio State University

Which is not linear operator?

If Y is the set R of real or C of complex numbers, then a non-linear operator is called a non-linear functional. The simplest example of a non-linear operator (non-linear functional) is a real-valued function of a real argument other than a linear function. 6 thg 6, 2020

Keywords People Search

• How do you show an operator is linear?
• Non-linear operator – Encyclopedia of Mathematics

What is linear operator with examples?

Examples: The simplest linear operator is the identity operator I. I|V> = |V>,

Keywords People Search

• How do you find the linear operator?
• Linear Operators

What is linear operator in vector space?

A linear operator T on a vector space V is a function that takes V to V with the properties: 1. T(u + v) = Tu + Tv, for all u, v ∈ V . 21 thg 10, 2013

Keywords People Search

• How do you find the linear operator?
• linear algebra: vector spaces and operators – MIT OpenCourseWare

What does the wave function Ψ represent?

Wave Functions. A wave function (Ψ) is a mathematical function that relates the location of an electron at a given point in space (identified by x, y, and z coordinates) to the amplitude of its wave, which corresponds to its energy. 2 thg 2, 2022

Keywords People Search

• What does solving Schrodinger equation mean?
• 8.6: Wave Mechanics – Chemistry LibreTexts

How did Schrodinger come up with his equation?

His great discovery, Schrödinger’s wave equation, was made at the end of this epoch-during the first half of 1926. It came as a result of his dissatisfaction with the quantum condition in Bohr’s orbit theory and his belief that atomic spectra should really be determined by some kind of eigenvalue problem.

Keywords People Search

• What does solving Schrodinger equation mean?
• Erwin Schrödinger – Facts – NobelPrize.org

How do you use Schrodinger?

Updating

Keywords People Search

• What does solving Schrodinger equation mean?
• Schrodinger equation | Derivation and how to use it – YouTube

Which of the following is known as the Schrödinger equation?

Schrodinger equation is written as HΨ = EΨ, where h is said to be a Hamiltonian operator.

Keywords People Search

• How do you find the Schrodinger equation?
• Schrodinger Wave Equation – Definition, Derivation, Significance

Which of the following is known as the Schrodinger equation?

The Schrödinger equation, sometimes called the Schrödinger wave equation, is a partial differential equation. It uses the concept of energy conservation (Kinetic Energy + Potential Energy = Total Energy) to obtain information about the behavior of an electron bound to a nucleus.

Keywords People Search

• How do you find the Schrodinger equation?
• Definition of the Schrödinger Equation – Chemistry Dictionary – Chemicool

Is Schrodinger equation true?

The Schroedinger Equation is the most true thing I’ve ever encountered. It is clear, simple, obvious in its correctness; the greatest piece of physics since Maxwell. Once you’ve understood it it becomes almost impossible to imagine that the universe could possibly work any other way. 11 thg 1, 2021

Keywords People Search

• How do you find the Schrodinger equation?
• Is the Schrödinger Equation True? | Hacker News

What are the eigenstates and eigenvalues of the Hamiltonian?

When discussing the eigenstates of the Hamiltonian (ˆH), the associated eigenvalues represent energies and within the context of the momentum operators, the associated eigenvalues refer to the momentum of the particle. 8 thg 9, 2021

Keywords People Search

• What does the Hamiltonian operator represent?
• 3.3: The Schrödinger Equation is an Eigenvalue Problem

Which physical quantity is represented by Hamiltonian operator?

The Hamiltonian corresponds to the energy of the system. 17 thg 12, 2020

Keywords People Search

• What does the Hamiltonian operator represent?
• What physical quantity does the Hamiltonian operator represent?

How do you use a Hamiltonian operator?

Updating

Keywords People Search

• What does the Hamiltonian operator represent?
• The Hamiltonian – YouTube

What is the significance of PSI and psi2?

PSI represents the amplitude of the electron wave. It is commonly called wave function. It is a mathematical function and has no physical meaning by itself. Magnitude of psi square has the physical meaning as it determines the probability of density of finding the electron at that point. 26 thg 8, 2019

Keywords People Search

• What is the physical significance of Sai square?
• What is the significance of psi and psi square chemistry? – Brainly.in

What is the significance of Ψ and ψ2 in quantum mechanical model of atom?

The wave function, ψ, is also called an atomic orbital. While the wave function, ψ, has no physical meaning, the square of the wave function, ψ2, is does. probability that the electron will be found at a particular location in an atom. particular location.

Keywords People Search

• What is the physical significance of Sai square?
• Chem 103, Section F0F Lecture 7 – The Quantum Mec

What is the significance of PSI and PSI 2?

Therefore the square of Ψ i.e., Ψ2 has a physical significance. In electron wave, Ψ2 gives the intensity of electron at any point. In other words Ψ2 helps in assessing the probability of electron in particular region, Thus Ψ2 is called probability density and Y is called probability amplitude. 12 thg 3, 2022

Keywords People Search

• What is the physical significance of Sai square?
• Explain the significance of Psi and Psi^(2) ? – Doubtnut

What is physical significance?

Physical significance of something is when you can see it in the real world. For example, the physical significance of time is that things age. The physical significance of friction is that things wear out.

Keywords People Search

• What is the physical significance of PSI square?
• What is the physical significance of mean? – Quora

What is Ψ * in physics?

Ψ∗ denotes the complex conjugate. Cite. Follow this answer to receive notifications. 8 thg 1, 2012

Keywords People Search

• What is the physical significance of PSI square?
• What does Ψ∗ mean in Schrodinger’s formulation of Quantum Mechanics?

What type of function is psi?

wave function The most common symbols for a wave function are the Greek letters ψ and Ψ (lower-case and capital psi, respectively). The wave function is a function of the degrees of freedom corresponding to some maximal set of commuting observables.

Keywords People Search

• What is the physical significance of PSI square?
• Wave function – Wikipedia

What are eigenvalues and eigenfunctions?

Such an equation, where the operator, operating on a function, produces a constant times the function, is called an eigenvalue equation. The function is called an eigenfunction, and the resulting numerical value is called the eigenvalue. 22 thg 7, 2021

Keywords People Search

• What is the significance of Ψ and ψ2 in quantum mechanical model of atom?
• 3.4: Operators, Eigenfunctions, Eigenvalues, and Eigenstates

What is a orbital How will you differentiate between an orbit and an orbital?

An orbit is the fixed path along which electrons revolve around the nucleus of the atom. … Differences between Orbit and Orbitals An orbit is the simple planar representation of an electron. An orbital refers to the dimensional motion of an electron around the nucleus in a three-dimensional motion. 4 hàng khác • 20 thg 9, 2019

Keywords People Search

• What is the significance of Ψ and ψ2 in quantum mechanical model of atom?
• Difference between Orbit and Orbitals – Key Differences with Examples

What are the significance of SIE and Sie square?

The wave function psi by itself have no physical Significance. It shows the amplitude of electron wave ( wave function). However its square that measures the probability of finding electron of giving energy from place to place in a giving region around the nucleus.

Keywords People Search

• What is the significance of Ψ and ψ2 in quantum mechanical model of atom?
• What is significance of psi and psi square? – Quora

What does the Hamiltonian operator represent?

In quantum mechanics, the Hamiltonian of a system is an operator corresponding to the total energy of that system, including both kinetic energy and potential energy.

Keywords People Search

• What is the expression for the Hamiltonian operator Mcq?
• Hamiltonian (quantum mechanics) – Wikipedia

When two operators commute What can we say about their eigenfunctions?

If two operators commute and consequently have the same set of eigenfunctions, then the corresponding physical quantities can be evaluated or measured exactly simultaneously with no limit on the uncertainty. 18 thg 3, 2020

Keywords People Search

• What is the expression for the Hamiltonian operator Mcq?
• 4.6: Commuting Operators Allow Infinite Precision

Which of the following is the correct expression for the orbital angular momentum Mcq?

Which of the following is the correct expression for the orbital angular momentum? Explanation: The orbital angular momentum of an electron is given by the expression: \sqrt{l(l+1)}. Thus, when the azimuthal quantum number, l, is zero the angular momentum is zero as well.

Keywords People Search

• What is the expression for the Hamiltonian operator Mcq?
• Engineering Physics Questions and Answers – Quantum Number

What is Lagrangian in classical mechanics?

For conservative systems, there is an elegant formulation of classical mechanics known as the Lagrangian formulation. The Lagrangian function, L, for a system is defined to be the difference between the kinetic and potential energies expressed as a function of positions and velocities. 15 thg 8, 2020

Keywords People Search

• What is Hamilton equation?
• The Lagrangian formulation of classical mechanics

How do you write the Lagrange equation?

One of the best known is called Lagrange’s equations. The Lagrangian L is defined as L = T − V, where T is the kinetic energy and V the potential energy of the system in question. 7 thg 2, 2022

Keywords People Search

• What is Hamilton equation?
• mechanics – Lagrange’s and Hamilton’s equations | Britannica

How do you write Lagrangian?

The Lagrangian is L = T −V = m ˙y2/2−mgy, so eq. (6.22) gives ¨y = −g, which is simply the F = ma equation (divided through by m), as expected. The solution is y(t) = −gt2/2+v0t+y0, as we well know.

Keywords People Search

• What is Hamilton equation?
• The Lagrangian Method

How do you find eigenvalues and eigenfunctions of an operator?

Updating

Keywords People Search

• What are the eigenstates and eigenvalues of the Hamiltonian?
• Quantum Chemistry 3.3 – Eigenvalues and Eigenfunctions – YouTube

What are the eigenstates of the Hamiltonian?

A system prepared in an eigenstate of the Hamiltonian has time-invariant probability density. A system prepared in an eigenstate of a non-commuting operator has a probability density which varies in time. It is this time independence (conservation law) which makes eigenstates of the energy operator so useful.

Keywords People Search

• What are the eigenstates and eigenvalues of the Hamiltonian?
• 1 Summary of things you should already know

What is the eigenvalue of the Hamiltonian operator?

The Hamiltonian operator, H ^ ψ = E ψ , extracts eigenvalue E from eigenfunction ψ, in which ψ represents the state of a system and E its energy. The expression H ^ ψ = E ψ is Schrödinger’s time-independent equation. In this chapter, the Hamiltonian operator will be denoted by. (74)

Keywords People Search

• What are the eigenstates and eigenvalues of the Hamiltonian?
• Hamiltonian Operator – an overview | ScienceDirect Topics

Which of the following are eigenfunctions of the momentum operator?

Ψ(x) is the eigenfunction of the momentum operator with the eigenvalue λ = − ℏ k \lambda = -\hbar k λ=−ℏk. 4 thg 6, 2021

Keywords People Search

• What are the eigenvalues and eigenfunctions?
• Answer to Question #203210 in Physics for Vinod Kumar

Which of the following functions are eigenfunctions of the operator D DX?

Which of the following is Eigen function of D DX? The function eax is aneigenfunction of the operator d/dx because (d/dx)eax ¼ aeax, which is a constant (a) multiplying the original function. … The constant o in an eigenvalueequation is called theeigenvalue of the operator O. 22 thg 12, 2020

Keywords People Search

• What are the eigenvalues and eigenfunctions?
• which of the following functions are eigen functions of d2/dx2. 1). Sin3x.

How do you show eigenfunctions are orthogonal?

Multiply the first equation by φ∗ and the second by ψ and integrate. If a1 and a2 in Equation 4.5. 14 are not equal, then the integral must be zero. This result proves that nondegenerate eigenfunctions of the same operator are orthogonal. 18 thg 3, 2020

Keywords People Search

• What are the eigenvalues and eigenfunctions?
• 4.5: Eigenfunctions of Operators are Orthogonal – Chemistry LibreTexts

What do you mean by eigenfunctions?

In mathematics, an eigenfunction of a linear operator D defined on some function space is any non-zero function in that space that, when acted upon by D, is only multiplied by some scaling factor called an eigenvalue.

Keywords People Search

• What are eigenfunctions and eigenvalues in chemistry?
• Eigenfunction – Wikipedia

What do you mean by eigenfunctions in chemistry?

An eigenfunction of an operator is a function such that the application of on gives. again, times a constant.

Keywords People Search

• What are eigenfunctions and eigenvalues in chemistry?
• Eigenfunctions and Eigenvalues

What are eigenvalues and eigenfunctions quantum mechanics?

In the case of Schrodinger’s equation, the eigenvalues are the possible energies that the system can have if it is in a state of well-defined energy. Each eigenfunction (of the Hamiltonian) is the state of the system when its energy is equal to the associated eigenvalue. 6 thg 12, 2018

Keywords People Search

• What are eigenfunctions and eigenvalues in chemistry?
• What is eigenvalue and eigenfunction in quantum mechanics?

Which of the following wave functions are eigenfunctions of the operator d2 dx2?

cos(3x) is an eigenfunction of the operator d2/dx2.

Keywords People Search

• What do you mean by eigenfunctions and eigenvalues in physics?
• The foundations of quantum mechanics

What is an observable operator?

An observable is an operator that corresponds to a physical quantity, such as. energy, spin, or position, that can be measured; think of a measuring device. with a pointer from which you can read off a real number which is the outcome. of the measurement. For a k-state quantum system, observables correspond.

Keywords People Search

• Is Hamiltonian an observable?
• Observables – EECS Instructional Support

What makes an operator observable?

In quantum physics, observables manifest as linear operators on a Hilbert space representing the state space of quantum states. The eigenvalues of observables are real numbers that correspond to possible values the dynamical variable represented by the observable can be measured as having.

Keywords People Search

• Is Hamiltonian an observable?
• Observable – Wikipedia

What is the difference between observable and operator?

An operator is usually a linear function from the Hilbert space of states to itself (although one also encounters the time reversal operator, which is anti-linear). An observable is a Hermitian linear operator that we can in principle measure, so all observables are operators, but not vice versa.

Keywords People Search

• Is Hamiltonian an observable?
• What is the difference between observables and operators … – Quora

How do you know if an operator is linear?

A function f is called a linear operator if it has the two properties: f(x+y)=f(x)+f(y) for all x and y; f(cx)=cf(x) for all x and all constants c.

Keywords People Search

• Is the Hamiltonian a linear operator?
• Linear operator | Glossary | Underground Mathematics

What is a linear operator in quantum mechanics?

Linear Operators. A linear operator is an instruction for transforming any given vector |V> in V into another vector |V’> in V while obeying the following rules: If Ω is a linear operator and a and b are elements of F then. Ωα|V> = αΩ|V>, Ω(α|Vi> + β|Vj>)= αΩ|Vi> + βΩ|Vj>.

Keywords People Search

• Is the Hamiltonian a linear operator?
• Linear Operators

What does it mean to be Hamiltonian?

Definition of Hamiltonian : a function that is used to describe a dynamic system (such as the motion of a particle) in terms of components of momentum and coordinates of space and time and that is equal to the total energy of the system when time is not explicitly part of the function — compare lagrangian.

Keywords People Search

• Is the Hamiltonian a linear operator?
• Hamiltonian Definition & Meaning – Merriam-Webster

What are the types of operator?

There are three types of operator that programmers use: arithmetic operators. relational operators. logical operators.

Keywords People Search

• What are the operators?
• Operators – Data types and structures – GCSE Computer Science Revision

What is an example of an operator?

The definition of an operator is someone who controls a machine, or the manager or owner of a business. An example of an operator is a person who controls a telephone switchboard. An example of an operator is someone who controls a crane at a loading dock.

Keywords People Search

• What are the operators?
• Operator Meaning | Best 27 Definitions of Operator

What is an operator explain different types of operators?

Operators can be defined as basic symbols that help us work on logical and mathematical operations. Operators in C and C++, are tools or symbols that are used to perform mathematical operations concerning arithmetic, logical, conditional and, bitwise operations. 21 thg 8, 2019

Keywords People Search

• What are the operators?
• 6 Types of Operators in C and C++ | Enhance Your Fundamental Skills …

What is the eigen value when the eigen function EX * is operated on the operator D DX?

a^ne^x is the eigen value of the function e^ax when operated on the operator d^n/dx^n. 19 thg 10, 2020

Keywords People Search

• What is Eigen value and eigen function in quantum mechanics?
• What is the eigen value of the function e^ax when operated on … – Brainly.in

How do you find the eigenvalue of an operator?

For a given linear operator T : V → V , a nonzero vector x and a constant scalar λ are called an eigenvector and its eigenvalue, respec- tively, when T(x) = λx. For a given eigenvalue λ, the set of all x such that T(x) = λx is called the λ-eigenspace.

Keywords People Search

• What is Eigen value and eigen function in quantum mechanics?
• Eigenvalues, eigenvectors, and eigenspaces of linear operators …

How do you find the eigenvalues of a Hamiltonian matrix?

To find the eigenvalues E we set the determinant of the matrix (H – EI) equal to zero and solve for E. To find the corresponding eigenvectors {|Ψ>}, we substitute each eigenvalue E back into the equation (H-E*I)|Ψ> = 0 and solve for the expansion coefficients of |Ψ> in the given basis.

Keywords People Search

• How do you find the eigenvalue of an operator?
• Eigenvalues

show that the spherical harmonics are eigenfunctions of the operator – Orbital angular momentum eigenfunctions

Watch The Video Below

Pictures on the topic show that the spherical harmonics are eigenfunctions of the operator | Orbital angular momentum eigenfunctions

What are the eigenstates and eigenvalues of the Hamiltonian?

When discussing the eigenstates of the Hamiltonian (ˆH), the associated eigenvalues represent energies and within the context of the momentum operators, the associated eigenvalues refer to the momentum of the particle. 8 thg 9, 2021

Keywords People Search

• How do you find the eigenvalue of an operator?
• 3.3: The Schrödinger Equation is an Eigenvalue Problem

What are the operators?

In mathematics and sometimes in computer programming, an operator is a character that represents an action, as for example x is an arithmetic operator that represents multiplication. In computer programs, one of the most familiar sets of operators, the Boolean operators, is used to work with true/false values.

Keywords People Search

• How do you find the eigenvalue of an operator?
• What is operator? – Definition from WhatIs.com

What is operator in quantum mechanics give example?

Table of QM operators Operator (common name/s) Cartesian component General definition Momentum Electromagnetic field Electromagnetic field (uses kinetic momentum; A, vector potential) Kinetic energy Translation Electromagnetic field Electromagnetic field (A, vector potential) Rotation (I, moment of inertia) Rotation 9 hàng khác

Keywords People Search

• What is an operator in quantum mechanics?
• Operator (physics) – Wikipedia

What is the name of operator?

Assignment operators Operator name Syntax C++ prototype examples Outside class definitions Bitwise OR assignment a |= b a or_eq b R& operator |=(K& a, S b); Bitwise XOR assignment a ^= b a xor_eq b R& operator ^=(K& a, S b); Bitwise left shift assignment a <<= b R& operator <<=(K& a, S b); 8 hàng khác

Keywords People Search

• What is an operator in quantum mechanics?
• Operators in C and C++ – Wikipedia

How do you show an operator is unitary?

We say U : V −→ V is unitary or a unitary operator if U∗ = U−1. A complex matrix A ∈ Mnn(C) is unitary if A∗ = A−1. A real matrix A ∈ Mnn(C) is orthogonal if AT = A−1.

Keywords People Search

• What is an operator in quantum mechanics?
• Lecture 38: Unitary operators – UNSW

Related searches

• show that lx, ly = ihlz
• completeness relation spherical harmonics
• spherical harmonics pdf
• introduction to spherical harmonics
• eigenvalues of lx and ly
• spherical harmonics orthogonality proof
• spherical harmonics – chemistry
• lz operator in spherical coordinates
• spherical harmonics chemistry
• show that lx ly ihlz

You have just come across an article on the topic show that the spherical harmonics are eigenfunctions of the operator. If you found this article useful, please share it. Thank you very much.