Let’s discuss the question: how many of the following relations are functions. We summarize all relevant answers in section Q&A of website Countrymusicstop.com in category: MMO. See more related questions in the comments below.
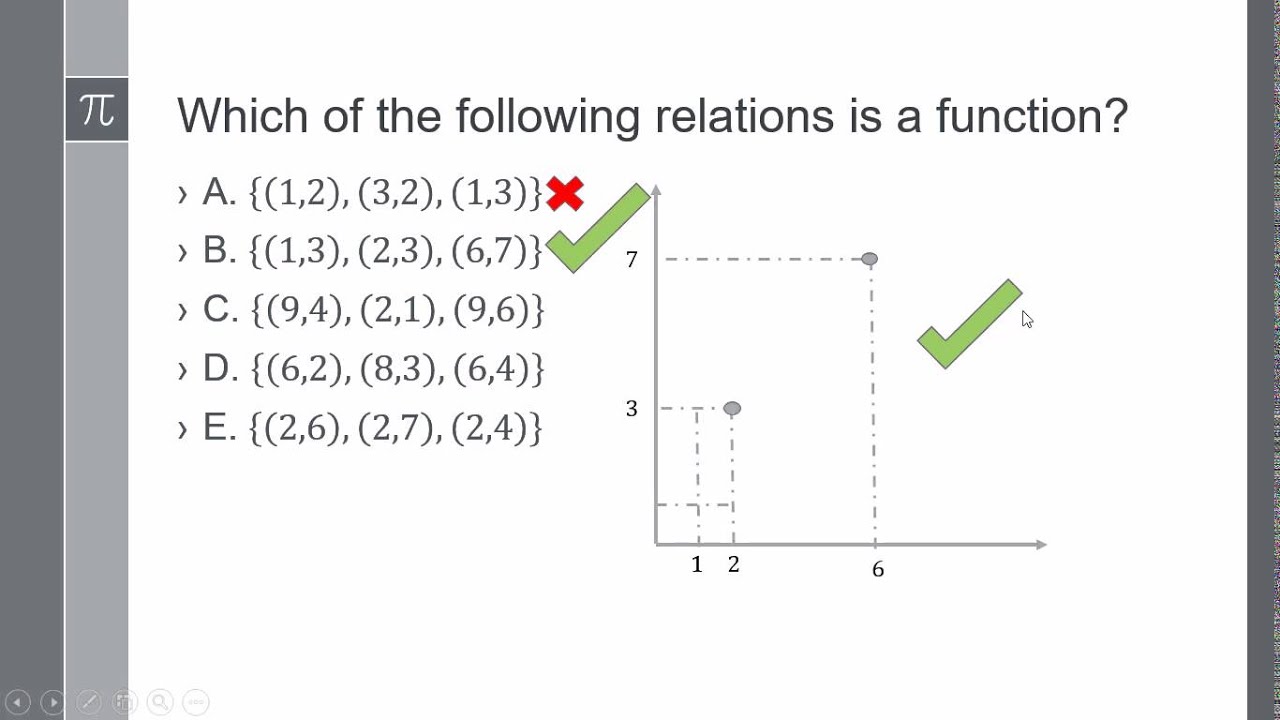
Table of Contents
How many relations are functions?
Functions can be one-to-one relations or many-to-one relations. A many-to-one relation associates two or more values of the independent (input) variable with a single value of the dependent (output) variable.
Which of following relations are functions?
Since 2, 5, 8, 11, 14, and 17 are the elements of the domain of the given relation having their unique images, this relation is a function. Since 2, 4, 6, 8, 10, 12 and 14 are the elements of the domain of the given relation having their unique images, this relation is a function.
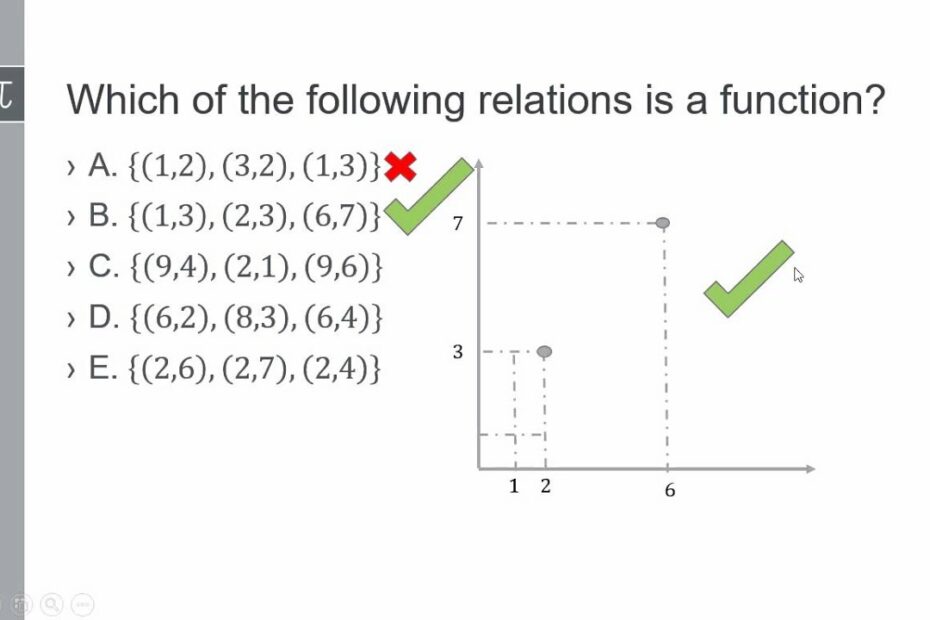
Which of the following relations is a function?
Images related to the topicWhich of the following relations is a function?

How do you determine if the following relations are functions?
Use the vertical line test to determine whether or not a graph represents a function. If a vertical line is moved across the graph and, at any time, touches the graph at only one point, then the graph is a function. If the vertical line touches the graph at more than one point, then the graph is not a function.
What are the types of relations in functions?
There are different types of relations and functions such as empty relation, universal relation, reflexive relation, symmetric relation, transitive relation, equivalence relation, constant function, polynomial function, identity function, on-to-one function, onto function, bijective function, etc.
What is a many to many function?
A relation can also be one to manyor many to many- where x values can have more than one y value. • A circle is an example of this of a many to many function. • A vertical line can cut through this graph more than once.
Is many-to-one relation a function?
Any function is either one-to-one or many-to-one. A function cannot be one-to-many because no element can have multiple images.
Is the given relation r 1 3 1 5 2 5 a function give reason if it is a function determine its domain and range?
Since the element 1 corresponds to two different images i.e., 3 and 5 . So, this relation is not a function.
Which of the following functions define the volume of a cube?
V=2s3 , where us is the length of the edge a. V= s/3 , where is is the length of the edge.
How can you say that an equation is a function?
A function is an equation that has only one answer for y for every x. A function assigns exactly one output to each input of a specified type. It is common to name a function either f(x) or g(x) instead of y. f(2) means that we should find the value of our function when x equals 2.
Is y 4 a function?
The answer would be yes since it passes the vertical line test. The vertical line test tells us if we draw a vertical line through any point of the graph and it goes through only one point at each line, then it is a function.
Relations \u0026 Functions
Images related to the topicRelations \u0026 Functions

Are all function relations?
All functions are relations, but not all relations are functions. A function is a relation that for each input, there is only one output. Here are mappings of functions. The domain is the input or the x-value, and the range is the output, or the y-value.
Is y 3 a function?
1 Answer. George C. Yes. The equation y=3 represents the function that maps all x values to 3 .
What are the 4 types of functions?
The types of functions can be broadly classified into four types. Based on Element: One to one Function, many to one function, onto function, one to one and onto function, into function.
How many relations are there?
There are 9 types of relations in maths namely: empty relation, full relation, reflexive relation, irreflexive relation, symmetric relation, anti-symmetric relation, transitive relation, equivalence relation, and asymmetric relation.
What is a function in relations and functions?
A function is a relation in which each input has only one output. In the relation , y is a function of x, because for each input x (1, 2, 3, or 0), there is only one output y. x is not a function of y, because the input y = 3 has multiple outputs: x = 1 and x = 2.
What is a many-to-many relationship example?
A many-to-many relationship occurs when multiple records in a table are associated with multiple records in another table. For example, a many-to-many relationship exists between customers and products: customers can purchase various products, and products can be purchased by many customers.
What relations are not functions?
Vertical lines are not functions. The equations y=±√x and x2+y2=9 are examples of non-functions because there is at least one x-value with two or more y-values.
What are the types of function?
- One – one function (Injective function)
- Many – one function.
- Onto – function (Surjective Function)
- Into – function.
- Polynomial function.
- Linear Function.
- Identical Function.
- Quadratic Function.
How do you find the domain of a function in class 11?
When the given function is of the form f(x) = 2x + 5 or f(x) = x2 – 2, the domain will be “the set of all real numbers. When the given function is of the form f(x) = 1/(x – 1), the domain will be the set of all real numbers except 1.
Relations and functions | Functions and their graphs | Algebra II | Khan Academy
Images related to the topicRelations and functions | Functions and their graphs | Algebra II | Khan Academy

Which of the following is an example of one to one relation?
Here are some examples of one-to-one relationships in the home: One family lives in one house, and the house contains one family. One person has one passport, and the passport can only be used by one person. One person has one ID number, and the ID number is unique to one person.
What is the range of the function shown by?
Step-by-step explanation:
Because the domain refers to the set of possible input values, the domain of a graph consists of all the input values shown on the x-axis. The range is the set of possible output values, which are shown on the y-axis.
Related searches
- what relations are functions
- does this relation give a function
- in a relation what do you call the set of x values or the input
- what are the rules of a function
- how to find the relation of a function
- which of the following relations is also a function
- Which of the following is a function
- which of the following relations are functions
- which of the following is a function
- is each relation a function
- which of the following relations is a function quizizz
- which of the following relations is a function brainly
- what is a function in relations
- which of the following relations is not a function
- does the relation define a function calculator
- which of the following relations is a function calculator
- in a relation what do you call the set of x-values or the input
Information related to the topic how many of the following relations are functions
Here are the search results of the thread how many of the following relations are functions from Bing. You can read more if you want.
You have just come across an article on the topic how many of the following relations are functions. If you found this article useful, please share it. Thank you very much.