Laplace Approximation Marginal Likelihood? Update New

Let’s discuss the question: “laplace approximation marginal likelihood?” We summarize all relevant answers in section Q&A of website Countrymusicstop.com. See more related questions in the comments below.

What is the Laplace approximation?

The term ‘Laplace approximation’ is used for the method of approximating a posterior distribution with a Gaussian centred at the maximum a posteriori (MAP) estimate. This is the application of Laplace’s method with f(θ) = p(λ\θ)p(θ).

Keywords People Search

laplace approximation marginal likelihood
Laplace Approximation – an overview | ScienceDirect Topics

laplace approximation marginal likelihood – BDA 2019 Lecture 11.1 Normal approximation, Laplace approximation.

Watch The Video Below

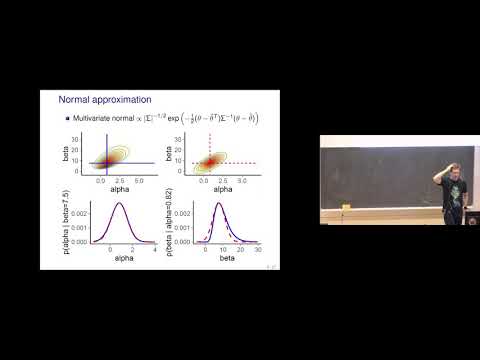
Pictures on the topic laplace approximation marginal likelihood | BDA 2019 Lecture 11.1 Normal approximation, Laplace approximation.

How is marginal likelihood calculated?

Marginal likelihood is the likelihood computed by “marginalizing” out the parameter θ : for each possible value that the parameter θ can have, we compute the likelihood at that value and multiply that likelihood with the probability/density of that θ value occurring.

Keywords People Search

laplace approximation marginal likelihood
The marginal likelihood (integrating out a parameter) | An Introduction to …

What is marginal likelihood function?

In statistics, a marginal likelihood function, or integrated likelihood, is a likelihood function in which some parameter variables have been marginalized. In the context of Bayesian statistics, it may also be referred to as the evidence or model evidence.

Keywords People Search

laplace approximation marginal likelihood
Marginal likelihood – Wikipedia

Why is the Laplace approximation equal to the exact posterior distribution?

Because h(θ) is simply a monotonic transformation of a function proportional to the posterior density, we know that h(θ) achieves its maximum at the posterior mode. Hence, the Laplace approximation to the posterior mean is equal to the posterior mode.

Keywords People Search

laplace approximation marginal likelihood
5.1 Laplace Approximation | Advanced Statistical Computing

What is integrated nested Laplace approximation?

The Integrated Nested Laplace Approximation (INLA) is a deterministic approach to Bayesian inference on latent Gaussian models (LGMs) and focuses on fast and accurate approximation of posterior marginals for the parameters in the models. 3 thg 3, 2021

Keywords People Search

What is the Laplace approximation?
[2103.02721] Importance Sampling with the Integrated Nested Laplace …

How do you do Laplace Transform?

Updating

Keywords People Search

What is the Laplace approximation?
Calculating a Laplace Transform – YouTube

What is the difference between likelihood and probability?

Probability refers to the chance that a particular outcome occurs based on the values of parameters in a model. Likelihood refers to how well a sample provides support for particular values of a parameter in a model. 18 thg 8, 2021

Keywords People Search

How is marginal likelihood calculated?
Likelihood vs. Probability: What’s the Difference? – Statology

What is the marginal likelihood for a Bayesian probabilistic model?

Marginal likelihoods are the currency of model comparison in a Bayesian framework. This differs from the frequentist approach to model choice, which is based on comparing the maximum probability or density of the data under two models either using a likelihood ratio test or some information-theoretic criterion.

Keywords People Search

How is marginal likelihood calculated?
Marginal Likelihoods in Phylogenetics: A Review of Methods and …

Can marginal likelihood be negative?

It follows that their product cannot be negative. The natural logarithm function is negative for values less than one and positive for values greater than one. So yes, it is possible that you end up with a negative value for log-likelihood (for discrete variables it will always be so). 17 thg 5, 2018

Keywords People Search

How is marginal likelihood calculated?
Can log likelihood function be negative – Cross Validated

What is EM algorithm used for?

The EM algorithm is used to find (local) maximum likelihood parameters of a statistical model in cases where the equations cannot be solved directly. Typically these models involve latent variables in addition to unknown parameters and known data observations.

Keywords People Search

What is marginal likelihood function?
Expectation–maximization algorithm – Wikipedia

How are posterior odds calculated?

If the prior odds are 1 / (N – 1) and the likelihood ratio is (1 / p) × (N – 1) / (N – n), then the posterior odds come to (1 / p) / (N – n).

Keywords People Search

What is marginal likelihood function?
Calculating the posterior odds from a single-match DNA database search

Is Bayes factor better than P value?

The short answer is Yes- the Bayes factor is really better than the p-value. The main reason is that the P-value (classic statistical inferences) simply answers a wrong hypothetical question that we only use as an unfortunate substitute for the actual question of interest.

Keywords People Search

What is marginal likelihood function?
Is Bayes Factor really better than p-value? – ResearchGate

How do you calculate Gaussian distribution?

The standard normal distribution (z distribution) is a normal distribution with a mean of 0 and a standard deviation of 1. Any point (x) from a normal distribution can be converted to the standard normal distribution (z) with the formula z = (x-mean) / standard deviation.

Keywords People Search

Why is the Laplace approximation equal to the exact posterior distribution?
Normal Distribution and Standard Normal (Gaussian) – StatsDirect

What is posterior mode?

The posterior mean and posterior mode are the mean and mode of the posterior. distribution of Θ; both of these are commonly used as a Bayesian estimate ˆθ for θ.

Keywords People Search

Why is the Laplace approximation equal to the exact posterior distribution?
Lecture 20 — Bayesian analysis 20.1 Prior and posterior distributions

How do I use INLA?

The general setup of an INLA spatial analysis is as follows: Plot and explore your data. Decide on covariates. Carry out model selection using DIC to reduce the number of covariates. Run a final non-spatial model. Decide on a set of spatial dependence structures.

Keywords People Search

What is integrated nested Laplace approximation?
Intro to modelling using INLA – Coding Club

What is Inlabru?

inlabru is hosted on Github, which provides an interface to report and track bugs, as well as instructions for installing newer bugfix releases and the current development version. If you encounter a problem please report it here. Report abuse. Report abuse.

Keywords People Search

What is integrated nested Laplace approximation?
inlabru

What is the difference between Fourier and Laplace transform?

Fourier transform is defined only for functions defined for all the real numbers, whereas Laplace transform does not require the function to be defined on set the negative real numbers. Every function that has a Fourier transform will have a Laplace transform but not vice-versa. 7 thg 12, 2011

Keywords People Search

How do you do Laplace Transform?
Difference Between Laplace and Fourier Transforms | Compare the …

What is the advantage of Laplace transform?

The advantage of using the Laplace transform is that it converts an ODE into an algebraic equation of the same order that is simpler to solve, even though it is a function of a complex variable. 26 thg 1, 2016

Keywords People Search

How do you do Laplace Transform?
Laplace Transforms and Linear Systems – Wiley Online Library

What is the Laplace transform of 0?

THe Laplace transform of e^(-at) is 1/s+a so 1 = e(-0t), so its transform is 1/s. Added after 2 minutes: so for 0, we got e^(-infinity*t), so for 0 it is 0. 8 thg 10, 2006

Keywords People Search

How do you do Laplace Transform?
Laplace Transform for x(t)=0? | Forum for Electronics

What is likelihood in stats?

Likelihood function is a fundamental concept in statistical inference. It indicates how likely a particular population is to produce an observed sample. Let P(X; T) be the distribution of a random vector X, where T is the vector of parameters of the distribution.

Keywords People Search

What is the difference between likelihood and probability?
Likelihood Function – Statistics.com

Is likelihood same as conditional probability?

A critical difference between probability and likelihood is in the interpretation of what is fixed and what can vary. In the case of a conditional probability, P(D|H), the hypothesis is fixed and the data are free to vary. Likelihood, however, is the opposite. 15 thg 4, 2015

Keywords People Search

What is the difference between likelihood and probability?
Understanding Bayes: A Look at the Likelihood | The Etz-Files

What is likelihood in machine learning?

One of the most commonly encountered way of thinking in machine learning is the maximum likelihood point of view. This is the concept that when working with a probabilistic model with unknown parameters, the parameters which make the data have the highest probability are the most likely ones.

Keywords People Search

What is the difference between likelihood and probability?
18.7. Maximum Likelihood – Dive into Deep Learning

What is the negative log likelihood?

Negative log-likelihood minimization is a proxy problem to the problem of maximum likelihood estimation. Cross-entropy and negative log-likelihood are closely related mathematical formulations. The essential part of computing the negative log-likelihood is to “sum up the correct log probabilities.” 8 thg 3, 2022

Keywords People Search

What is the marginal likelihood for a Bayesian probabilistic model?
Cross-Entropy, Negative Log-Likelihood, and All That Jazz

How do you compare Bayesian models?

So to compare two models we just compute the Bayesian log likelihood of the model and the model with the highest value is more likely. If you have more than one model you just compare all the models to each other pairwise and the model with the highest Bayesian log likelihood is the best. 6 thg 8, 2010

Keywords People Search

What is the marginal likelihood for a Bayesian probabilistic model?
Bayesian model comparison | Scientific Clearing House

What is Bayesian model selection?

Bayesian model selection uses the rules of probability theory to select among different hypotheses. It is completely analogous to Bayesian classification. It automatically encodes a preference for simpler, more constrained models, as illustrated at right. 23 thg 9, 2005

Keywords People Search

What is the marginal likelihood for a Bayesian probabilistic model?
Bayesian model selection – MIT alumni

Is higher log likelihood better?

The higher the value of the log-likelihood, the better a model fits a dataset. The log-likelihood value for a given model can range from negative infinity to positive infinity. The actual log-likelihood value for a given model is mostly meaningless, but it’s useful for comparing two or more models. 31 thg 8, 2021

Keywords People Search

Can marginal likelihood be negative?
How to Interpret Log-Likelihood Values (With Examples) – Statology

Can a maximum likelihood estimate be negative?

As maximum likelihood estimates cannot be negative, they will be found at the boundary of the parameter space (ie, it is 0). (6) Maximizing ℓ over the parameters π can be done using an EM algorithm, or by maximizing the likelihood directly (compare Van den Hout and van der Heijden, 2002).

Keywords People Search

Can marginal likelihood be negative?
Maximum Likelihood Estimate – an overview | ScienceDirect Topics

What is a good positive likelihood ratio?

A relatively high likelihood ratio of 10 or greater will result in a large and significant increase in the probability of a disease, given a positive test. A LR of 5 will moderately increase the probability of a disease, given a positive test. 1 thg 2, 2011

Keywords People Search

Can marginal likelihood be negative?
Likelihood Ratios

What are the disadvantages of the EM algorithm?

Disadvantages of EM algorithm – It has slow convergence. It makes convergence to the local optima only. It requires both the probabilities, forward and backward (numerical optimization requires only forward probability). 14 thg 5, 2019

Keywords People Search

What is EM algorithm used for?
ML | Expectation-Maximization Algorithm – GeeksforGeeks

What is the difference between K mean and EM?

EM and K-means are similar in the sense that they allow model refining of an iterative process to find the best congestion. However, the K-means algorithm differs in the method used for calculating the Euclidean distance while calculating the distance between each of two data items; and EM uses statistical methods.

Keywords People Search

What is EM algorithm used for?
Clustering performance comparison using K-means and expectation …

What is true about EM algorithm?

The EM algorithm is an iterative approach that cycles between two modes. The first mode attempts to estimate the missing or latent variables, called the estimation-step or E-step. The second mode attempts to optimize the parameters of the model to best explain the data, called the maximization-step or M-step. 1 thg 11, 2019

Keywords People Search

What is EM algorithm used for?
A Gentle Introduction to Expectation-Maximization (EM …

What is the difference between the likelihood and the posterior probability?

To put simply, likelihood is “the likelihood of θ having generated D” and posterior is essentially “the likelihood of θ having generated D” further multiplied by the prior distribution of θ. 3 thg 10, 2019

Keywords People Search

How are posterior odds calculated?
What is the conceptual difference between posterior and likelihood?

What is Frequentist vs Bayesian?

Frequentist statistics never uses or calculates the probability of the hypothesis, while Bayesian uses probabilities of data and probabilities of both hypothesis. Frequentist methods do not demand construction of a prior and depend on the probabilities of observed and unobserved data.

Keywords People Search

How are posterior odds calculated?
Bayes or not Bayes, is this the question? – PMC – NCBI

What is the difference between prior and posterior probabilities?

Prior probability represents what is originally believed before new evidence is introduced, and posterior probability takes this new information into account.

Keywords People Search

How are posterior odds calculated?
Posterior Probability Definition – Investopedia

Is 0.08 statistically significant?

The numerical result 0.08 shows a non-significant test.

Keywords People Search

Is Bayes factor better than P value?
Hello everyone! How can I interpret a p-value of test (F) = 0.08 in a pooled …

What does a probability of 0.05 mean?

P > 0.05 is the probability that the null hypothesis is true. 1 minus the P value is the probability that the alternative hypothesis is true. A statistically significant test result (P ≤ 0.05) means that the test hypothesis is false or should be rejected. A P value greater than 0.05 means that no effect was observed. 10 thg 8, 2016

Keywords People Search

Is Bayes factor better than P value?
“P < 0.05” Might Not Mean What You Think: American Statistical ... - NCBI

Is p-value 0.1 significant?

The smaller the p-value, the stronger the evidence for rejecting the H0. This leads to the guidelines of p < 0.001 indicating very strong evidence against H0, p < 0.01 strong evidence, p < 0.05 moderate evidence, p < 0.1 weak evidence or a trend, and p ≥ 0.1 indicating insufficient evidence[1].

Keywords People Search

Is Bayes factor better than P value?
What is a P-value? – Biosci

What is the difference between Gaussian and normal distribution?

Normal distribution, also known as the Gaussian distribution, is a probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean. In graph form, normal distribution will appear as a bell curve.

Keywords People Search

How do you calculate Gaussian distribution?
Normal Distribution Definition – Investopedia

Is Gaussian distribution discrete or continuous?

The rectified Gaussian distribution replaces negative values from a normal distribution with a discrete component at zero. The compound poisson-gamma or Tweedie distribution is continuous over the strictly positive real numbers, with a mass at zero.

Keywords People Search

How do you calculate Gaussian distribution?
List of probability distributions – Wikipedia

What is the difference between Gaussian and Poisson distribution?

The Poisson distribution takes on values for 0, 1, 2, 3, and so on because of its discrete nature, whereas the Gaussian function is continuously varying over all possible values, including values less than zero if the mean is small (eg, µ = 4). …

Keywords People Search

How do you calculate Gaussian distribution?
Difference between Gaussian and Poisson distributions. Graph shows …

What is the maximum a posterior MAP estimate of θ?

Maximum A Posteriori Estimation. MLE is powerful when you have enough data. However, it doesn’t work well when observed data size is small. For example, if Liverpool only had 2 matches and they won the 2 matches, then the estimated value of θ by MLE is 2/2 = 1. 11 thg 6, 2019

Keywords People Search

What is posterior mode?
A Gentle Introduction to Maximum Likelihood Estimation and …

What are the parameters of gamma distribution?

The gamma distribution is the maximum entropy probability distribution (both with respect to a uniform base measure and with respect to a 1/x base measure) for a random variable X for which E[X] = kθ = α/β is fixed and greater than zero, and E[ln(X)] = ψ(k) + ln(θ) = ψ(α) − ln(β) is fixed (ψ is the digamma function).

Keywords People Search

What is posterior mode?
Gamma distribution – Wikipedia

What is beta prior?

In the literature you’ll see that the beta distribution is called a conjugate prior for the binomial distribution. This means that if the likelihood function is binomial, then a beta prior gives a beta posterior. In fact, the beta distribution is a conjugate prior for the Bernoulli and geometric distributions as well.

Keywords People Search

What is posterior mode?
Reading 14a: Beta Distributions – MIT OpenCourseWare

What is an INLA stack?

inla.stack: Data stacking for advanced INLA models in andrewzm/INLA: Functions which allow to perform full Bayesian analysis of latent Gaussian models using Integrated Nested Laplace Approximaxion. 10 thg 5, 2019

Keywords People Search

How do I use INLA?
inla.stack: Data stacking for advanced INLA models – Rdrr.io

How do I download an INLA in R?

The INLA package can be obtained from . We recommend the testing version, which can be downloaded by running: install. packages(“INLA”, repos=c(getOption(“repos”), INLA=”https://inla.r-inla-download.org/R/testing”), dep=TRUE). 30 thg 11, 2021

Keywords People Search

How do I use INLA?
CRAN – Package meta4diag

What is integrated nested Laplace approximation?

Keywords People Search

How do I use INLA?
[2103.02721] Importance Sampling with the Integrated Nested Laplace …

What is relation between DFT and Z transform?

Let x(n) be a discrete sequence. Hence, Fourier Transform of a discrete signal is equal to Z− Transform evaluated on a unit circle. From Part I and II, DFT of a discrete signal is equal to Z−Transform evaluated on a unit circle calculated at discrete instant of Frequency.

Keywords People Search

What is the difference between Fourier and Laplace transform?
State the relationship between DFS, DFT and Z Transform – Ques10

What is difference between DFT and Dtft?

A DFT sequence has periodicity, hence called periodic sequence with period N. A DTFT sequence contains periodicity, hence called periodic sequence with period 2π. The DFT can be calculated in computers as well as in digital processors as it does not contain any continuous variable of frequency. 3 thg 4, 2021

Keywords People Search

What is the difference between Fourier and Laplace transform?
Difference between DFT and DTFT | Electricalvoice

What is ROC in Laplace transform?

Properties of ROC of Laplace Transform ROC contains strip lines parallel to jω axis in s-plane. If x(t) is absolutely integral and it is of finite duration, then ROC is entire s-plane. If x(t) is a right sided sequence then ROC : Re{s} > σo.

Keywords People Search

What is the difference between Fourier and Laplace transform?
Region of Convergence (ROC) – Tutorialspoint

What are the disadvantages of Laplace transform?

Laplace transform & its disadvantages a. Unsuitability for data processing in random vibrations. b. Analysis of discontinuous inputs. c. Possibility of conversion s = jω is only for sinusoidal steady state analysis. d. Inability to exist for few Probability Distribution Functions. 6 thg 10, 2015

Keywords People Search

What is the advantage of Laplace transform?
Laplace transform & its disadvantages – Career Ride

What is the importance of application of the Laplace transform to the analysis of circuits with initial conditions?

Similar to the application of phasor transform to solve the steady state AC circuits , Laplace transform can be used to transform the time domain circuits into S domain circuits to simplify the solution of integral differential equations to the manipulation of a set of algebraic equations.

Keywords People Search

What is the advantage of Laplace transform?
laplace transform and its application in circuit analysis

What is the main advantage of using Laplace transforms for circuit analysis versus using traditional circuit analysis?

For the domain of circuit analysis the use of laplace transforms allows us to solve the differential equations that represent these circuits through the application of simple rules and algebraic processes instead of more complex mathematical techniques. It also gives insight into circuit behaviour. 23 thg 9, 2019

Keywords People Search

What is the advantage of Laplace transform?
How is Laplace transform used in circuit analysis? – Rampfesthudson …

What is the Laplace transform of f/t 1?

Calculate the Laplace Transform of the function f(t)=1 This is one of the easiest Laplace Transforms to calculate: Integrate e^(-st)*f(t) from t =0 to infinity: => [-exp(-st)/s] evaluated at inf – evaluated at 0 => 0 – (-1/s) = 1/s ! 28 thg 9, 2017

Keywords People Search

What is the Laplace transform of 0?
Calculate the Laplace Transform of the function f(t)=1 – Wyzant

Can you take the Laplace transform of a constant?

In general, if a function of time is multiplied by some constant, then the Laplace transform of that function is multiplied by the same constant. Thus, if we have a step input of size 5 at time t=0 then the Laplace transform is five times the transform of a unit step and so is 5/s.

Keywords People Search

What is the Laplace transform of 0?
Laplace Transforms – an overview | ScienceDirect Topics

What is the Laplace transform of E at?

Derivation: f(t) F(s) ROC e-at 1 s + a Re (s) > -a t e-at 1 ( s + a ) 2 Re (s) > -a tn e-at n ! ( s + a ) n Re (s) > -a Sin at a s 2 + a 2 Re (s) > 0 5 hàng khác

Keywords People Search

What is the Laplace transform of 0?
[Solved] The Laplace transform of e-at is: – Testbook.com

How do you find the likelihood?

The likelihood function is given by: L(p|x) ∝p4(1 − p)6. The likelihood of p=0.5 is 9.77×10−4, whereas the likelihood of p=0.1 is 5.31×10−5.

Keywords People Search

What is likelihood in stats?
Lecture notes on likelihood function

Is likelihood the same as probability density?

A probability density function (pdf) is a non-negative function that integrates to 1. The likelihood is defined as the joint density of the observed data as a function of the parameter. 27 thg 6, 2012

Keywords People Search

What is likelihood in stats?
What is the reason that a likelihood function is not a pdf?

How is likelihood different from probability?

Keywords People Search

Is likelihood same as conditional probability?
Likelihood vs. Probability: What’s the Difference? – Statology

What is likelihood in stats?

Keywords People Search

Is likelihood same as conditional probability?
Likelihood Function – Statistics.com

What is maximum likelihood in machine learning?

Keywords People Search

What is likelihood in machine learning?
18.7. Maximum Likelihood – Dive into Deep Learning

What is maximum likelihood in ML?

In statistics, maximum likelihood estimation (MLE) is a method of estimating the parameters of an assumed probability distribution, given some observed data. This is achieved by maximizing a likelihood function so that, under the assumed statistical model, the observed data is most probable.

Keywords People Search

What is likelihood in machine learning?
Maximum likelihood estimation – Wikipedia

Is a higher negative log likelihood better?

The higher the value of the log-likelihood, the better a model fits a dataset. The log-likelihood value for a given model can range from negative infinity to positive infinity. 31 thg 8, 2021

Keywords People Search

What is the negative log likelihood?
How to Interpret Log-Likelihood Values (With Examples) – Statology

What is a negative 2 log likelihood?

The Deviance (-2LL) statistic The deviance, or -2 log-likelihood (-2LL) statistic, can help us here. The deviance is basically a measure of how much unexplained variation there is in our logistic regression model – the higher the value the less accurate the model. 22 thg 7, 2011

Keywords People Search

What is the negative log likelihood?
4.6 How good is the model? – ReStore

What is HDI Bayesian?

2 Bayesian HDI. A concept in Bayesian inference, that is somewhat analogous to the NHST CI, is the HDI, which was introduced in Section 4.3. 4, p. 87. The 95% HDI consists of those values of θ that have at least some minimal level of posterior credibility, such that the total probability of all such θ values is 95%.

Keywords People Search

How do you compare Bayesian models?
Highest Density Interval – an overview | ScienceDirect Topics

What is Bayesian evidence?

Bayesian inference is a method of statistical inference in which Bayes’ theorem is used to update the probability for a hypothesis as more evidence or information becomes available. Bayesian inference is an important technique in statistics, and especially in mathematical statistics.

Keywords People Search

How do you compare Bayesian models?
Bayesian inference – Wikipedia

How is BIC calculated?

The BIC statistic is calculated for logistic regression as follows (taken from “The Elements of Statistical Learning“): BIC = -2 * LL + log(N) * k. 30 thg 10, 2019

Keywords People Search

What is Bayesian model selection?
Probabilistic Model Selection with AIC, BIC, and MDL

What is Bayesian data analysis?

Bayesian analysis, a method of statistical inference (named for English mathematician Thomas Bayes) that allows one to combine prior information about a population parameter with evidence from information contained in a sample to guide the statistical inference process.

Keywords People Search

What is Bayesian model selection?
Bayesian analysis | statistics – Encyclopedia Britannica

What is an acceptable log likelihood?

Log-likelihood values cannot be used alone as an index of fit because they are a function of sample size but can be used to compare the fit of different coefficients. Because you want to maximize the log-likelihood, the higher value is better. For example, a log-likelihood value of -3 is better than -7.

Keywords People Search

Is higher log likelihood better?
What is log-likelihood? – Minitab – Support

What is a good likelihood ratio?

Keywords People Search

Is higher log likelihood better?
Likelihood Ratios

Can marginal likelihood be negative?

Keywords People Search

Can a maximum likelihood estimate be negative?
Can log likelihood function be negative – Cross Validated

Can a likelihood interval have negative value?

The 95% confidence interval is providing a range that you are 95% confident the true difference in means falls in. Thus, the CI can include negative numbers, because the difference in means may be negative. 16 thg 4, 2015

Keywords People Search

Can a maximum likelihood estimate be negative?
How to interpret negative 95% confidence interval? – Cross Validated

What is LR+ and LR?

LR+ = Probability that a person with the disease tested positive/probability that a person without the disease tested positive. i.e., LR+ = true positive/false positive. LR− = Probability that a person with the disease tested negative/probability that a person without the disease tested negative.

Keywords People Search

What is a good positive likelihood ratio?
Understanding the properties of diagnostic tests – Part 2: Likelihood …

What does an LR+ between 5 and 10 mean?

Interpretation: Positive Likelihood Ratio (LR+) LR+ over 5 – 10: Significantly increases likelihood of the disease. LR+ between 0.2 to 5 (esp if close to 1): Does not modify the likelihood of the disease. LR+ below 0.1 – 0.2: Significantly decreases the likelihood of the disease.

Keywords People Search

What is a good positive likelihood ratio?
Likelihood Ratio – Family Practice Notebook

What is EM in statistics?

In statistics, an expectation–maximization (EM) algorithm is an iterative method to find (local) maximum likelihood or maximum a posteriori (MAP) estimates of parameters in statistical models, where the model depends on unobserved latent variables.

Keywords People Search

What are the disadvantages of the EM algorithm?
Expectation–maximization algorithm – Wikipedia

What problem does the EM algorithm solve?

The Expectation-Maximization Algorithm, or EM algorithm for short, is an approach for maximum likelihood estimation in the presence of latent variables. A general technique for finding maximum likelihood estimators in latent variable models is the expectation-maximization (EM) algorithm. 1 thg 11, 2019

Keywords People Search

What are the disadvantages of the EM algorithm?
A Gentle Introduction to Expectation-Maximization (EM …

Why is EM better than K-means?

Keywords People Search

What is the difference between K mean and EM?
Clustering performance comparison using K-means and expectation …

Does K mean EM?

k-means is a variant of EM, with the assumptions that clusters are spherical. 2 thg 12, 2013

Keywords People Search

What is the difference between K mean and EM?
Clustering with K-Means and EM: how are they related? – Cross Validated

Is expectation maximization unsupervised learning?

Expectation Maximization (EM) is a classic algorithm developed in the 60s and 70s with diverse applications. It can be used as an unsupervised clustering algorithm and extends to NLP applications like Latent Dirichlet Allocation¹, the Baum–Welch algorithm for Hidden Markov Models, and medical imaging. 11 thg 7, 2020

Keywords People Search

What is true about EM algorithm?
Expectation Maximization Explained | by Ravi Charan – Towards Data …

Does EM algorithm always converge?

So yes, EM algorithm always converges, even though it might converge to bad local extrema, which is a different issue. 25 thg 9, 2012

Keywords People Search

What is true about EM algorithm?
How to prove the convergence of EM? [closed] – Stack Overflow

What is prior posterior and likelihood?

Prior: Probability distribution representing knowledge or uncertainty of a data object prior or before observing it. Posterior: Conditional probability distribution representing what parameters are likely after observing the data object. Likelihood: The probability of falling under a specific category or class.

Keywords People Search

What is the difference between the likelihood and the posterior probability?
Prior, likelihood, and posterior – Machine Learning with Spark

Is likelihood the same as conditional probability?

Conditional probability is defined as the likelihood of an event or outcome occurring, based on the occurrence of a previous event or outcome. Conditional probability is calculated by multiplying the probability of the preceding event by the updated probability of the succeeding, or conditional, event.

Keywords People Search

What is the difference between the likelihood and the posterior probability?
Conditional Probability Definition – Investopedia

Is frequentist or Bayesian better?

For the groups that have the ability to model priors and understand the difference in the answers that Bayesian gives versus frequentist approaches, Bayesian is usually better, though it can actually be worse on small data sets.

Keywords People Search

What is Frequentist vs Bayesian?
Bayesian vs. Frequentist A/B Testing: What’s the Difference? – CXL

Is P value a Frequentist probability?

The traditional frequentist definition of a p-value is, roughly, the probability of obtaining results which are as inconsistent or more inconsistent with the null hypothesis as the ones you obtained. 7 thg 8, 2017

Keywords People Search

What is Frequentist vs Bayesian?
How can one express frequentist p-value in terms of Bayesian …

What is a good posterior probability?

The corresponding confidence measures in phylogenetics are posterior probabilities and bootstrap and aLRTS. Values of probability of 0.95 or 0.99 are considered really strong evidence for monoplyly of a clade.

Keywords People Search

What is the difference between prior and posterior probabilities?
What is the recommended value of posterior probability in Mr. Bayes …

What does the prior probability represent?

What Is Prior Probability? Prior probability, in Bayesian statistical inference, is the probability of an event before new data is collected. This is the best rational assessment of the probability of an outcome based on the current knowledge before an experiment is performed.

Keywords People Search

What is the difference between prior and posterior probabilities?
Prior Probability – Investopedia

Is p-value of 0.05 significant?

A p-value less than 0.05 (typically ≤ 0.05) is statistically significant. It indicates strong evidence against the null hypothesis, as there is less than a 5% probability the null is correct (and the results are random).

Keywords People Search

Is 0.08 statistically significant?
P-Value and Statistical Significance – Simply Psychology

laplace approximation marginal likelihood – Introducing Bayes factors and marginal likelihoods

Watch Video Now

Pictures on the topic laplace approximation marginal likelihood | Introducing Bayes factors and marginal likelihoods

What does AP value greater than 0.05 mean?

Keywords People Search

Is 0.08 statistically significant?
“P < 0.05” Might Not Mean What You Think: American Statistical ... - NCBI

Is p 0.01 statistically significant?

For example, a p-value that is more than 0.05 is considered statistically significant while a figure that is less than 0.01 is viewed as highly statistically significant.

Keywords People Search

What does a probability of 0.05 mean?
P-value – Definition, How To Use, and Misinterpretations

What does p-value of 0.001 mean?

1 in a thousand The p-value indicates how probable the results are due to chance. p=0.05 means that there is a 5% probability that the results are due to random chance. p=0.001 means that the chances are only 1 in a thousand. The choice of significance level at which you reject null hypothesis is arbitrary.

Keywords People Search

What does a probability of 0.05 mean?
P Value, Statistical Significance and Clinical Significance

What is a 1% level of significance?

Use in Practice. Popular levels of significance are 10% (0.1), 5% (0.05), 1% (0.01), 0.5% (0.005), and 0.1% (0.001). If a test of significance gives a p-value lower than or equal to the significance level, the null hypothesis is rejected at that level.

Keywords People Search

Is p-value 0.1 significant?
A Closer Look at Tests of Significance | Boundless Statistics

What is the difference between 0.01 and 0.05 level of significance?

Probability between 0.01 and 0.05: Evidence. Probability between 0.001 and 0.01: Strong evidence. Probability < 0.001: Very strong evidence. 6 thg 11, 2016

Keywords People Search

Is p-value 0.1 significant?
Should my alpha be set to .05 or .01? – ResearchGate

Is Gaussian normalized?

The Gaussian distribution is a continuous function which approximates the exact binomial distribution of events. The Gaussian distribution shown is normalized so that the sum over all values of x gives a probability of 1.

Keywords People Search

What is the difference between Gaussian and normal distribution?
Gaussian Distribution Function – HyperPhysics

How do you know if data is Gaussian?

You can test the hypothesis that your data were sampled from a Normal (Gaussian) distribution visually (with QQ-plots and histograms) or statistically (with tests such as D’Agostino-Pearson and Kolmogorov-Smirnov). 30 thg 8, 2021

Keywords People Search

What is the difference between Gaussian and normal distribution?
How do I know if my data have a normal distribution? – FAQ 2185

What is the difference between Gaussian and normal distribution?

Keywords People Search

Is Gaussian distribution discrete or continuous?
Normal Distribution Definition – Investopedia

Is Gaussian random variable continuous?

A continuous random variable Z is said to be a standard normal (standard Gaussian) random variable, shown as Z∼N(0,1), if its PDF is given by fZ(z)=1√2πexp{−z22},for all z∈R.

Keywords People Search

Is Gaussian distribution discrete or continuous?
Normal Distribution | Gaussian | Normal random variables | PDF

Is Poisson distribution discrete or continuous?

discrete distribution The Poisson distribution is a discrete distribution that measures the probability of a given number of events happening in a specified time period.

Keywords People Search

What is the difference between Gaussian and Poisson distribution?
Poisson Distribution – an overview | ScienceDirect Topics

Is Poisson a Gaussian?

Keywords People Search

What is the difference between Gaussian and Poisson distribution?
Difference between Gaussian and Poisson distributions. Graph shows …

What is maximum posterior hypothesis in machine learning?

In Bayesian statistics, a maximum a posteriori probability (MAP) estimate is an estimate of an unknown quantity, that equals the mode of the posterior distribution. The MAP can be used to obtain a point estimate of an unobserved quantity on the basis of empirical data.

Keywords People Search

What is the maximum a posterior MAP estimate of θ?
Maximum a posteriori estimation – Wikipedia

How do you calculate posterior mode?

The posterior mean is then (s+α)/(n+2α), and the posterior mode is (s+α−1)/(n+2α−2). Both of these may be taken as a point estimate p for p. The interval from the 0.05 to the 0.95 quantile of the Beta(s+α, n−s+α) distribution forms a 90% Bayesian credible interval for p. Example 20.5.

Keywords People Search

What is the maximum a posterior MAP estimate of θ?
Lecture 20 — Bayesian analysis 20.1 Prior and posterior distributions

How do you interpret gamma distribution?

Gamma Distribution is a Continuous Probability Distribution that is widely used in different fields of science to model continuous variables that are always positive and have skewed distributions. It occurs naturally in the processes where the waiting times between events are relevant. 25 thg 6, 2020

Keywords People Search

What are the parameters of gamma distribution?
Gamma Distribution Explained | What is Gamma Distribution?

What is the standard deviation of a gamma distribution?

Gamma Distribution Mean γ Range 0 to \infty. Standard Deviation \sqrt{\gamma} Skewness \frac{2} {\sqrt{\gamma}} Kurtosis 3 + \frac{6} {\gamma} 2 hàng khác

Keywords People Search

What are the parameters of gamma distribution?
1.3.6.6.11. Gamma Distribution

What is beta in gamma distribution?

The effect of changing alpha and beta on the shape of the gamma distribution. You can think of α as the number of events you are waiting for (although α can be any positive number — not just integers), and β as the mean waiting time until the first event. 30 thg 1, 2014

Keywords People Search

What is beta prior?
Gamma Distribution: Definition, PDF, Finding in Excel – Statistics How To

What is alpha and beta in beta distribution?

Beta(α, β): the name of the probability distribution. B(α, β ): the name of a function in the denominator of the pdf. This acts as a “normalizing constant” to ensure that the area under the curve of the pdf equals 1. β: the name of the second shape parameter in the pdf. 5 thg 8, 2015

Keywords People Search

What is beta prior?
Beta Distribution: Definition, Calculation – Statistics How To

How do I use INLA?

Keywords People Search

What is an INLA stack?
Intro to modelling using INLA – Coding Club

How do I download an INLA in R?

Keywords People Search

What is an INLA stack?
CRAN – Package meta4diag

What is integrated nested Laplace approximation?

Keywords People Search

How do I download an INLA in R?
[2103.02721] Importance Sampling with the Integrated Nested Laplace …

What is the relationship between DFT and DFS?

The discrete Fourier series (DFS) is used to represent periodic time functions and the DFT is used to repre- sent finite-duration time functions.

Keywords People Search

What is relation between DFT and Z transform?
introduction to the dfs and the dft

How is Z transform obtained from Laplace transform?

In summary, the z transform (times the sampling interval T) of a discrete time signal xd(nT) approaches, as T → 0, the Laplace Transform of the underly- ing continuous-time signal xd(t). For the mapping z = esT from the s plane to the z plane to be invertible, it is necessary that X(jωa) be zero for all |ωa| ≥ π/T.

Keywords People Search

What is relation between DFT and Z transform?
The Laplace Transform Relation to the z Transform – CCRMA

Is DFS and DFT same?

Basically, DFS is used for periodic and infinite sequence. Whereas, DFT is used for non-periodic and finite sequence. Although, They are same Mathematically. 9 thg 5, 2014

Keywords People Search

What is relation between DFT and Z transform?
The difference between DFT and DFS – Signal Processing Stack Exchange

Why DFT is preferred over DTFT?

advantages of dft method DFT is completely discrete both in frequency and time, however DTFT is only discrete in time but continueous in frequency. DTFT is not used in actual digital signal processing, its DFT which is mostly calculated using fast algorithms called FFT algorithms. 2 thg 7, 2007

Keywords People Search

What is difference between DFT and Dtft?
what are the advantages of DFT over DTFT. | Forum for Electronics

Why we need DFT when we have DTFT?

The answer is the same to the question: “Why do we need computers to process data when we have paper and pencil?” DTFT as well as the continuous-time Fourier Transform is a theoretical tool for infinitely long hypothetical signals. the DFT is to observe the spectrum of actual data that is finite in size. 13 thg 12, 2020

Keywords People Search

What is difference between DFT and Dtft?
Why do we need DFT when we already have DTFT/DTFS?

Why DFT is used in DSP?

The Discrete Fourier Transform (DFT) is of paramount importance in all areas of digital signal processing. It is used to derive a frequency-domain (spectral) representation of the signal.

Keywords People Search

What is difference between DFT and Dtft?
Discrete Fourier Transform – an overview | ScienceDirect Topics

What is DFT and Idft?

The discrete Fourier transform (DFT) and its inverse (IDFT) are the primary numerical transforms relating time and frequency in digital signal processing. 20 thg 8, 2006

Keywords People Search

What is ROC in Laplace transform?
DFT Definition and Properties – Digital Signal Processing: A User’s Guide

What is ROC in control system?

The region of convergence, known as the ROC, is important to understand because it defines the region where the z-transform exists. The z-transform of a sequence is defined as. X(z)=∞∑n=−∞x[n]z−n. The ROC for a given x[n], is defined as the range of z for which the z-transform converges. 23 thg 2, 2021

Keywords People Search

What is ROC in Laplace transform?
12.6: Region of Convergence for the Z-Transform – Engineering LibreTexts

What is Z-transform in DSP?

In mathematics and signal processing, the Z-transform converts a discrete-time signal, which is a sequence of real or complex numbers, into a complex frequency-domain representation. It can be considered as a discrete-time analogue of the Laplace transform.

Keywords People Search

What is ROC in Laplace transform?
Z-transform – Wikipedia

What are the limitations of Fourier Transform?

The major disadvantage of the Fourier transformation is the inherent compromise that exists between frequency and time resolution. The length of Fourier transformation used can be critical in ensuring that subtle changes in frequency over time, which are very important in bat echolocation calls, are seen.

Keywords People Search

What are the disadvantages of Laplace transform?
Advantages and Disadvantages of Techniques for Transforming and …

Does Laplace transform of e’t 2 exist?

Existence of Laplace Transforms. for every real number s. Hence, the function f(t)=et2 does not have a Laplace transform. 21 thg 10, 2021

Keywords People Search

What are the disadvantages of Laplace transform?
8.1: Introduction to the Laplace Transform – Mathematics LibreTexts

What are benefits of applying Laplace transformation?

Keywords People Search

What are the disadvantages of Laplace transform?
Laplace Transforms and Linear Systems – Wiley Online Library

How is Laplace transform used in real life?

The transforms are used to study and analyze systems such as ventilation, heating and air conditions, etc. These systems are used in every single modern day construction and building. Laplace transforms are also important for process controls. 22 thg 10, 2020

Keywords People Search

What is the importance of application of the Laplace transform to the analysis of circuits with initial conditions?
Laplace Transform Table, Formula, Examples & Properties – Electrical4U

What is the main advantage of using laplace transforms for circuit analysis versus using traditional circuit analysis as done in earlier chapters?

Keywords People Search

What is the importance of application of the Laplace transform to the analysis of circuits with initial conditions?
How is Laplace transform used in circuit analysis? – Rampfesthudson …

What are the disadvantages of Laplace transform?

Keywords People Search

What is the importance of application of the Laplace transform to the analysis of circuits with initial conditions?
Laplace transform & its disadvantages – Career Ride

When can you use Laplace transform in circuits?

Laplace transform methods can be employed to study circuits in the s-domain. Laplace techniques convert circuits with voltage and current signals that change with time to the s-domain so you can analyze the circuit’s action using only algebraic techniques. 26 thg 3, 2016

Keywords People Search

What is the main advantage of using Laplace transforms for circuit analysis versus using traditional circuit analysis?
Laplace Transforms and s-Domain Circuit Analysis

What is the importance of application of the Laplace transform to the analysis of circuits with initial conditions?

Keywords People Search

What is the main advantage of using Laplace transforms for circuit analysis versus using traditional circuit analysis?
laplace transform and its application in circuit analysis

Why do we use Laplace transform in electrical engineering?

The Laplace Transform is a powerful tool that is very useful in Electrical Engineering. The transform allows equations in the “”time domain”” to be transformed into an equivalent equation in the Complex S Domain.

Keywords People Search

What is the main advantage of using Laplace transforms for circuit analysis versus using traditional circuit analysis?
Circuit Theory/Laplace Transform – Wikibooks, open books for an open …

What is the Laplace transform of sinat?

L[sinat] = a s2 + a2 .

Keywords People Search

What is the Laplace transform of f/t 1?
“JUST THE MATHS” UNIT NUMBER 16.1 LAPLACE TRANSFORMS 1 …

What is H in Laplace transform?

The switching property: Let H(t) be the Heaviside function: H(t) = {0 for t < 0, 1 for t ≥ 0, and F(s) be the Laplace transform of f(t).

Keywords People Search

What is the Laplace transform of f/t 1?
The Laplace Transform 1 1. The Laplace transform of a function f(t …

What is the Laplace transform of 0?

THe Laplace transform of e^(-at) is 1/s+a so 1 = e(-0t), so its transform is 1/s. Added after 2 minutes: so for 0, we got e^(-infinity*t), so for 0 it is 0. 8 thg 10, 2006

Keywords People Search

What is the Laplace transform of f/t 1?
Laplace Transform for x(t)=0? | Forum for Electronics

What is the value of parabolic input in Laplace transform?

The Laplace transform of a parabolic function is 1 s 3 . hence, statement 3 is also correct.

Keywords People Search

Can you take the Laplace transform of a constant?
Consider the following statements regarding a parabolic function

What is the difference between Laplace and Fourier transform?

Keywords People Search

Can you take the Laplace transform of a constant?
Difference Between Laplace and Fourier Transforms | Compare the …

laplace approximation marginal likelihood – 6-4 Laplace Approximation | Python Kumar

Watch The Video Below

Pictures on the topic laplace approximation marginal likelihood | 6-4 Laplace Approximation | Python Kumar

What is the Laplace transform of f/t 1?

Keywords People Search

Can you take the Laplace transform of a constant?
Calculate the Laplace Transform of the function f(t)=1 – Wyzant

What is the Laplace transform of sin at?

What is the Laplace transform of sin t? The Laplace transform of f(t) = sin t is L{sin t} = 1/(s^2 + 1). As we know that the Laplace transform of sin at = a/(s^2 + a^2). 2 thg 10, 2020

Keywords People Search

What is the Laplace transform of E at?
Laplace Transform (Definition, Formula, Properties and Examples)

How do you find Laplace inverse?

A Laplace transform which is a constant multiplied by a function has an inverse of the constant multiplied by the inverse of the function. First shift theorem: L − 1 { F ( s − a ) } = e a t f ( t ) , where f(t) is the inverse transform of F(s).

Keywords People Search

What is the Laplace transform of E at?
Inverse Laplace Transform – an overview | ScienceDirect Topics

What does likeliness mean?

Definitions of likeliness. the probability of a specified outcome. synonyms: likelihood. Antonyms: unlikelihood, unlikeliness. the improbability of a specified outcome.

Keywords People Search

How do you find the likelihood?
Likeliness – Definition, Meaning & Synonyms | Vocabulary.com

What is likelihood in probability?

Probability is about a finite set of possible outcomes, given a probability. Likelihood is about an infinite set of possible probabilities, given an outcome. 31 thg 8, 2015

Keywords People Search

How do you find the likelihood?
Bayes for Beginners: Probability and Likelihood – Association for …

What is the likelihood of data?

In other words, we speak of the probability of data (given a model or hypothesis), or the likelihood of a model (given some data). Likelihood is proportional to the probability of observing the data given the hypothesis; this is similar to a p-value, but does not include the tail of the distribution.

Keywords People Search

How do you find the likelihood?
Likelihood Methods – Data Analysis in the Geosciences

Is likelihood proportional to probability?

Likelihood is a strange concept, in that it is not a probability, but it is proportional to a probability. The likelihood of a hypothesis (H) given some data (D) is proportional to the probability of obtaining D given that H is true, multiplied by an arbitrary positive constant K. In other words, L(H) = K × P(D|H).

Keywords People Search

Is likelihood the same as probability density?
Introduction to the concept of likelihood and its applications – OSF

Is likelihood a probability distribution?

Probability corresponds to finding the chance of something given a sample distribution of the data, while on the other hand, Likelihood refers to finding the best distribution of the data given a particular value of some feature or some situation in the data. 25 thg 11, 2020

Keywords People Search

Is likelihood the same as probability density?
Probability VS Likelihood – Medium

How is likelihood calculated?

Probability represents the likelihood of an event occurring for a fraction of the number of times you test the outcome. The odds take the probability of an event occurring and divide it by the probability of the event not occurring. 25 thg 3, 2021

Keywords People Search

Is likelihood the same as probability density?
How To Calculate Probability | Indeed.com

Is likelihood the same as probability density?

Keywords People Search

How is likelihood different from probability?
What is the reason that a likelihood function is not a pdf?

Is likelihood same as conditional probability?

Keywords People Search

How is likelihood different from probability?
Understanding Bayes: A Look at the Likelihood | The Etz-Files

What is the difference between likelihood and prior probability?

The likelihood is the joint density of the data, given a parameter value and the prior is the marginal distribution of the parameter. 20 thg 5, 2012

Keywords People Search

How is likelihood different from probability?
What is the difference between “”priors”” and “”likelihood””?

What is likelihood used for?

The likelihood function is that density interpreted as a function of the parameter (possibly a vector), rather than the possible outcomes. This provides a likelihood function for any statistical model with all distributions, whether discrete, absolutely continuous, a mixture or something else.

Keywords People Search

What is likelihood in stats?
Likelihood function – Wikipedia

What is Gibbs algorithm in machine learning?

Summary. Gibbs sampling is a Markov Chain Monte Carlo (MCMC) algorithm where each random variable is iteratively resampled from its conditional distribution given the remaining variables. It’s a simple and often highly effective approach for performing posterior inference in probabilistic models.

Keywords People Search

What is maximum likelihood in machine learning?
Gibbs sampling – Metacademy

How do you interpret maximum likelihood?

Updating

Keywords People Search

What is maximum likelihood in machine learning?
Maximum Likelihood, clearly explained!!! – YouTube

Is maximum likelihood estimator efficient?

It is easy to check that the MLE is an unbiased estimator (E[̂θMLE(y)] = θ). To determine the CRLB, we need to calculate the Fisher information of the model. Yk) = σ2 n . (6) So CRLB equality is achieved, thus the MLE is efficient. 27 thg 4, 2015

Keywords People Search

What is maximum likelihood in ML?
Lecture 8: Properties of Maximum Likelihood Estimation (MLE)

How do you calculate maximum likelihood?

Let X1, X2, X3, …, Xn be a random sample from a distribution with a parameter θ. Given that we have observed X1=x1, X2=x2, ⋯, Xn=xn, a maximum likelihood estimate of θ, shown by ˆθML is a value of θ that maximizes the likelihood function L(x1,x2,⋯,xn;θ). … Solution. θ PX1X2X3X4(1,0,1,1;θ) 0 0 1 0.0247 2 0.0988 3 0

Keywords People Search

What is maximum likelihood in ML?
Maximum Likelihood Estimation – Probability Course

Is a lower likelihood better?

Keywords People Search

Is a higher negative log likelihood better?
What is log-likelihood? – Minitab – Support

How do you interpret a negative log likelihood?

Negative Log-Likelihood (NLL) We can interpret the loss as the “unhappiness” of the network with respect to its parameters. The higher the loss, the higher the unhappiness: we don’t want that. We want to make our models happy. is 0, and reaches 0 when input is 1. 13 thg 8, 2017

Keywords People Search

Is a higher negative log likelihood better?
Understanding softmax and the negative log-likelihood – Lj Miranda

What does negative Loglikelihood mean?

Keywords People Search

What is a negative 2 log likelihood?
Cross-Entropy, Negative Log-Likelihood, and All That Jazz

Is a higher negative log likelihood better?

The higher the value of the log-likelihood, the better a model fits a dataset. The log-likelihood value for a given model can range from negative infinity to positive infinity. 31 thg 8, 2021

Keywords People Search

What is a negative 2 log likelihood?
How to Interpret Log-Likelihood Values (With Examples) – Statology

What is a 95 credible interval?

Interpretation of the Bayesian 95% confidence interval (which is known as credible interval): there is a 95% probability that the true (unknown) estimate would lie within the interval, given the evidence provided by the observed data. 31 thg 12, 2018

Keywords People Search

What is HDI Bayesian?
Understanding and interpreting confidence and credible intervals …

What is Frequentist vs Bayesian?

Keywords People Search

What is HDI Bayesian?
Bayes or not Bayes, is this the question? – PMC – NCBI

Why is Bayesian statistics important?

Bayesian statistics gives us a solid mathematical means of incorporating our prior beliefs, and evidence, to produce new posterior beliefs. Bayesian statistics provides us with mathematical tools to rationally update our subjective beliefs in light of new data or evidence.

Keywords People Search

What is Bayesian evidence?
Bayesian Statistics: A Beginner’s Guide | QuantStart

What are the basic characteristics of Bayesian theorem?

Bayes’ Theorem states that the conditional probability of an event, based on the occurrence of another event, is equal to the likelihood of the second event given the first event multiplied by the probability of the first event.

Keywords People Search

What is Bayesian evidence?
Bayes’ Theorem Definition – Investopedia

What is an acceptable BIC value?

If it’s between 6 and 10, the evidence for the best model and against the weaker model is strong. A Δ BIC of greater than ten means the evidence favoring our best model vs the alternate is very strong indeed. 10 thg 3, 2018

Keywords People Search

How is BIC calculated?
Bayesian Information Criterion (BIC) / Schwarz Criterion – Statistics How To

What is a low BIC?

Lower BIC value indicates lower penalty terms hence a better model. Read also AIC statistics. Though these two measures are derived from a different perspective, they are closely related. Apparently, the only difference is BIC considers the number of observations in the formula, which AIC does not.

Keywords People Search

How is BIC calculated?
What is Bayesian Information Criterion (BIC)? | by Analyttica Datalab

Should I take Bayesian Statistics?

Bayesian statistics is appropriate when you have incomplete information that may be updated after further observation or experiment. You start with a prior (belief or guess) that is updated by Bayes’ Law to get a posterior (improved guess).

Keywords People Search

What is Bayesian data analysis?
When should we apply Frequentist statistics and when … – ResearchGate

How hard is Bayesian Statistics?

Bayesian methods can be computationally intensive, but there are lots of ways to deal with that. And for most applications, they are fast enough, which is all that matters. Finally, they are not that hard, especially if you take a computational approach. 18 thg 5, 2016

Keywords People Search

What is Bayesian data analysis?
Learning to Love Bayesian Statistics – Probably Overthinking It

Is higher log likelihood better?

Many procedures use the log of the likelihood, rather than the likelihood itself, because it is easier to work with. The log likelihood (i.e., the log of the likelihood) will always be negative, with higher values (closer to zero) indicating a better fitting model.

Keywords People Search

What is an acceptable log likelihood?
How are the likelihood ratio, Wald, and Lagrange multiplier (score …

How do you interpret a log ratio?

Well, here’s how taking the log of the ratio works: A word has the same relative frequency in A and B – the binary log of the ratio is 0. A word is 2 times more common in A than in B – the binary log of the ratio is 1. A word is 4 times more common in A than in B – the binary log of the ratio is 2. Mục khác… • 28 thg 4, 2014

Keywords People Search

What is an acceptable log likelihood?
Log Ratio – an informal introduction

What does a negative likelihood ratio of 0.1 mean?

The negative likelihood ratio (-LR) gives the change in the odds of having a diagnosis in patients with a negative test. The change is in the form of a ratio, usually less than 1. For example, a -LR of 0.1 would indicate a 10-fold decrease in the odds of having a condition in a patient with a negative test result. 1 thg 2, 2011

Keywords People Search

What is a good likelihood ratio?
Likelihood Ratios

What does an LR+ between 5 and 10 mean?

Keywords People Search

What is a good likelihood ratio?
Likelihood Ratio – Family Practice Notebook

What is likelihood and marginal likelihood?

From Wikipedia, the free encyclopedia. In statistics, a marginal likelihood function, or integrated likelihood, is a likelihood function in which some parameter variables have been marginalized. In the context of Bayesian statistics, it may also be referred to as the evidence or model evidence.

Keywords People Search

Can marginal likelihood be negative?
Marginal likelihood – Wikipedia

What is EM algorithm used for?

Keywords People Search

Can marginal likelihood be negative?
Expectation–maximization algorithm – Wikipedia

Can marginal likelihood be negative?

Keywords People Search

Can a likelihood interval have negative value?
Can log likelihood function be negative – Cross Validated

What if a 95% confidence interval is negative?

In simple terms, a negative confidence interval in this setting means that although observation is that mean of group 2 is 0.028 higher than group 1, the 95% confidence interval suggest that actually group 1 may be higher than group 2. 16 thg 4, 2015

Keywords People Search

Can a likelihood interval have negative value?
How to interpret negative 95% confidence interval? – Cross Validated

What is a likelihood ratio of 1?

A LR close to 1 means that the test result does not change the likelihood of disease or the outcome of interest appreciably. The more the likelihood ratio for a positive test (LR+) is greater than 1, the more likely the disease or outcome.

Keywords People Search

What is LR+ and LR?
Likelihood ratios, predictive values, and post-test probabilities

How do you calculate LR and LR+?

The calculations are based on the following formulas: LR+ = sensitivity / 1- specificity. LR- = 1- sensitivity / specificity.

Keywords People Search

What is LR+ and LR?
Diagnostics and Likelihood Ratios, Explained – The NNT

What is LR+ and LR?

Keywords People Search

What does an LR+ between 5 and 10 mean?
Understanding the properties of diagnostic tests – Part 2: Likelihood …

What does a likelihood ratio of 0.5 mean?

Interpreting Likelihood Ratios A rule of thumb (McGee, 2002; Sloane, 2008) for interpreting them: 0 to 1: decreased evidence for disease. Values closer to zero have a higher decrease in probability of disease. For example, a LR of 0.1 decreases probability by -45%, while a value of -0.5 decreases probability by -15%. 14 thg 9, 2016

Keywords People Search

What does an LR+ between 5 and 10 mean?
Likelihood Ratio (Medicine): Basic Definition, Interpretation

What is the difference between K mean and EM?

Keywords People Search

What is EM in statistics?
Clustering performance comparison using K-means and expectation …

What is the log likelihood in EM algorithm?

In our EM algorithm, the expected complete data log-likelihood ( Q ) is a function of a set of model parameters τ, i.e. We maximize Q at each EM cycle by solving the equation that sets to zero its partial derivative w.r.t. each parameter.

Keywords People Search

What is EM in statistics?
Expected complete data log-likelihood and EM Estimation of …

Is EM algorithm monotonic?

It is now intuitively clear that EM based algorithms monotonically increase the data likelihood function, and that they converge with high probability to a local maximum of the likelihood function pZ (z ; θ) that depends on the starting point.

Keywords People Search

What is EM in statistics?
Expectation-Maximization (EM) Method – Springer

What is the relationship between maximum likelihood estimation MLE and expectation maximization EM algorithm?

Specifically, you learned: Maximum likelihood estimation is challenging on data in the presence of latent variables. Expectation maximization provides an iterative solution to maximum likelihood estimation with latent variables. 1 thg 11, 2019

Keywords People Search

What problem does the EM algorithm solve?
A Gentle Introduction to Expectation-Maximization (EM …

Is expectation maximization unsupervised learning?

Keywords People Search

What problem does the EM algorithm solve?
Expectation Maximization Explained | by Ravi Charan – Towards Data …

What is guaranteed to increase in every step of EM algorithm?

Advantages of EM algorithm – It is always guaranteed that likelihood will increase with each iteration. The E-step and M-step are often pretty easy for many problems in terms of implementation. 14 thg 5, 2019

Keywords People Search

What problem does the EM algorithm solve?
ML | Expectation-Maximization Algorithm – GeeksforGeeks

Does K mean EM?

k-means is a variant of EM, with the assumptions that clusters are spherical. 2 thg 12, 2013

Keywords People Search

Why is EM better than K-means?
Clustering with K-Means and EM: how are they related? – Cross Validated

Is K-means an EM algorithm?

Process of K-Means is something like assigning each observation to a cluster and process of EM(Expectation Maximization) is finding likelihood of an observation belonging to a cluster(probability). This is where both of these processes differ. 22 thg 5, 2019

Keywords People Search

Why is EM better than K-means?
What is the difference between K-mean and EM? How to decide k

Is K-means an expectation maximization?

Expectation Maximization works the same way as K-means except that the data is assigned to each cluster with the weights being soft probabilities instead of distances. The advantage is that the model becomes generative as we define the probability distribution for each model. 22 thg 2, 2018

Keywords People Search

Why is EM better than K-means?
Expectation Maximization. A peek into generative algorithms – Medium

What is the difference between K-means and Knn?

k-Means Clustering is an unsupervised learning algorithm that is used for clustering whereas KNN is a supervised learning algorithm used for classification. KNN is a classification algorithm which falls under the greedy techniques however k-means is a clustering algorithm (unsupervised machine learning technique).

Keywords People Search

Does K mean EM?
How is KNN different from k-means clustering? – ResearchGate

What is soft k?

K -means clustering is a method of clustering data represented as D -dimensional vectors. Specifically, there will be N items to be clustered, each represented as a vector yn∈RD y n ∈ R D . In the “soft” version of K -means, the assignments to clusters will be probabilistic.

Keywords People Search

Does K mean EM?
9.2 Soft \(K\)-Means | Stan User’s Guide

Is EM a clustering algorithm?

The EM algorithm extends this basic approach to clustering in two important ways: Instead of assigning examples to clusters to maximize the differences in means for continuous variables, the EM clustering algorithm computes probabilities of cluster memberships based on one or more probability distributions.

Keywords People Search

Does K mean EM?
Expectation Maximization Clustering – RapidMiner Documentation

Why does expectation maximization converge?

In the M-step, the likelihood function is maximized under the assumption that the missing data are known. The estimate of the missing data from the E-step are used in lieu of the actual missing data. Convergence is assured since the algorithm is guaranteed to increase the likelihood at each iteration.

Keywords People Search

Is expectation maximization unsupervised learning?
The Expectation Maximization Algorithm: A short tutorial

Does EM algorithm always converge?

So yes, EM algorithm always converges, even though it might converge to bad local extrema, which is a different issue. 25 thg 9, 2012

Keywords People Search

Is expectation maximization unsupervised learning?
How to prove the convergence of EM? [closed] – Stack Overflow

Is EM supervised or unsupervised?

Although EM is most useful in practice for lightly supervised data, it is more easily formulated for the case of unsupervised learning.

Keywords People Search

Is expectation maximization unsupervised learning?
Expectation Maximization (EM) 1 Hard EM – TTIC

Does EM converge to global maximum?

First of all, it is possible that EM converges to a local min, a local max, or a saddle point of the likelihood function. More precisely, as Tom Minka pointed out, EM is guaranteed to converge to a point with zero gradient. 26 thg 1, 2014

Keywords People Search

Does EM algorithm always converge?
Why is the Expectation Maximization algorithm guaranteed to converge …

Does the EM algorithm monotonically increases the likelihood of the data with each iteration?

Specifically, under some mild conditions, the EM algorithm is guaranteed to monotonically increase the observed data log likelihood at each iteration until it reaches a local maximum (or a saddle point). 21 thg 11, 2017

Keywords People Search

Does EM algorithm always converge?
a new EM style algorithm with partial E-steps – arXiv

Does GMM always converge?

It always converges, but it may converge at a local optimum that is different from the global optimum, and in fact could be arbitrarily worse in terms of its score. 20 thg 3, 2017

Keywords People Search

Does EM algorithm always converge?
K-‐Means + GMMs – Carnegie Mellon University School of Computer …

What is the difference between likelihood and prior probability?

Probability is used to finding the chance of occurrence of a particular situation, whereas Likelihood is used to generally maximizing the chances of a particular situation to occur. 25 thg 11, 2020

Keywords People Search

What is prior posterior and likelihood?
Probability VS Likelihood – Medium

What is prior probability and likelihood?

Keywords People Search

What is prior posterior and likelihood?
Prior, likelihood, and posterior – Machine Learning with Spark

What is meant by prior probability?

Prior probability, in Bayesian statistical inference, is the probability of an event before new data is collected. This is the best rational assessment of the probability of an outcome based on the current knowledge before an experiment is performed.

Keywords People Search

What is prior posterior and likelihood?
Prior Probability – Investopedia

Is likelihood the same as probability density?

Keywords People Search

Is likelihood the same as conditional probability?
What is the reason that a likelihood function is not a pdf?

How is likelihood calculated?

Keywords People Search

Is likelihood the same as conditional probability?
How To Calculate Probability | Indeed.com

Does likelihood sum to 1?

A likelihood distribution will not sum to one, because there is no reason for the sum or integral of likelihoods over all parameter values to sum to one. 13 thg 9, 2018

Keywords People Search

Is likelihood the same as conditional probability?
Probability and likelihood distributions | Species and Gene Evolution

Is P value a Frequentist probability?

Keywords People Search

Is frequentist or Bayesian better?
How can one express frequentist p-value in terms of Bayesian …

What is the disadvantage of Bayesian network?

Perhaps the most significant disadvantage of an approach involving Bayesian Networks is the fact that there is no universally accepted method for constructing a network from data.

Keywords People Search

Is frequentist or Bayesian better?
Strengths and Weaknesses of Bayesian Networks

Why is Bayesian statistics better than frequentist?

Keywords People Search

Is frequentist or Bayesian better?
Bayes or not Bayes, is this the question? – PMC – NCBI

What is frequentist hypothesis testing?

Most commonly-used frequentist hypothesis tests involve the following elements: Model assumptions (e.g., for the t-test for the mean, the model assumptions can be phrased as: simple random sample1 of a random variable with a normal distribution) Null and alternative hypothesis. A test statistic. 10 thg 5, 2012

Keywords People Search

Is P value a Frequentist probability?
Overview of Frequentist Hypothesis Testing

What is frequentist test?

The Frequentist approach It’s the model of statistics taught in most core-requirement college classes, and it’s the approach most often used by A/B testing software. Basically, a Frequentist method makes predictions on the underlying truths of the experiment using only data from the current experiment.

Keywords People Search

Is P value a Frequentist probability?
Bayesian vs. Frequentist A/B Testing: What’s the Difference? – CXL

Why is p value misinterpreted?

Common misinterpretations of single P values. ThePvalue is the probability that the test hypothesis is true; for example, if a test of the null hypothesis gaveP = 0.01, the null hypothesis has only a 1 % chance of being true; if instead it gaveP = 0.40, the null hypothesis has a 40 % chance of being true.

Keywords People Search

Is P value a Frequentist probability?
Statistical tests, P values, confidence intervals, and power: a guide to

How do you get prior posterior?

Posterior probability = prior probability + new evidence (called likelihood). For example, historical data suggests that around 60% of students who start college will graduate within 6 years. This is the prior probability. 4 thg 3, 2016

Keywords People Search

What is a good posterior probability?
Posterior Probability & the Posterior Distribution – Statistics How To

How are posterior odds calculated?

If the prior odds are 1 / (N – 1) and the likelihood ratio is (1 / p) × (N – 1) / (N – n), then the posterior odds come to (1 / p) / (N – n).

Keywords People Search

What is a good posterior probability?
Calculating the posterior odds from a single-match DNA database search

How is posterior probabilities calculated?

A posterior probability, in Bayesian statistics, is the revised or updated probability of an event occurring after taking into consideration new information. The posterior probability is calculated by updating the prior probability using Bayes’ theorem.

Keywords People Search

What is a good posterior probability?
Posterior Probability Definition – Investopedia

How is prior probability calculated?

The a priori probability of landing a head is calculated as follows: A priori probability = 1 / 2 = 50%. Therefore, the a priori probability of landing a head is 50%.

Keywords People Search

What does the prior probability represent?
A Priori Probability – Overview, Formula, Examples

What is prior probability probability distribution with sufficient evidence?

In Bayesian statistical inference, a prior probability distribution, often simply called the prior, of an uncertain quantity is the probability distribution that would express one’s beliefs about this quantity before some evidence is taken into account.

Keywords People Search

What does the prior probability represent?
Prior probability – Wikipedia

What does Bayes theorem calculate prior probability?

Bayes’ Theorem calculates the conditional probability of an event, based on the values of specific related known probabilities.

Keywords People Search

What does the prior probability represent?
Bayes’ Theorem Definition – Investopedia

Is p 0.01 statistically significant?

For example, a p-value that is more than 0.05 is considered statistically significant while a figure that is less than 0.01 is viewed as highly statistically significant.

Keywords People Search

Is p-value of 0.05 significant?
P-value – Definition, How To Use, and Misinterpretations

Is 0.06 statistically significant?

A p value of 0.06 means that there is a probability of 6% of obtaining that result by chance when the treatment has no real effect. Because we set the significance level at 5%, the null hypothesis should not be rejected.

Keywords People Search

Is p-value of 0.05 significant?
What does the p value really mean? – NCBI

Is 0.051 statistically significant?

How about 0.051? It’s still not statistically significant, and data analysts should not try to pretend otherwise. A p-value is not a negotiation: if p > 0.05, the results are not significant. 3 thg 12, 2015

Keywords People Search

Is p-value of 0.05 significant?
What Can You Say When Your P-Value is Greater Than 0.05?

What does p-value of 0.9 mean?

If P(real) = 0.9, there is only a 10% chance that the null hypothesis is true at the outset. Consequently, the probability of rejecting a true null at the conclusion of the test must be less than 10%. 1 thg 5, 2014

Keywords People Search

What does AP value greater than 0.05 mean?
Not All P Values are Created Equal – Minitab Blog

What does p-value of 0.5 mean?

Mathematical probabilities like p-values range from 0 (no chance) to 1 (absolute certainty). So 0.5 means a 50 per cent chance and 0.05 means a 5 per cent chance. In most sciences, results yielding a p-value of . 05 are considered on the borderline of statistical significance. If the p-value is under .

Keywords People Search

What does AP value greater than 0.05 mean?
Statistical significance – Institute for Work & Health

Why do we use 0.05 level of significance?

For example, a significance level of 0.05 indicates a 5% risk of concluding that a difference exists when there is no actual difference. Lower significance levels indicate that you require stronger evidence before you will reject the null hypothesis.

Keywords People Search

What does AP value greater than 0.05 mean?
Significance level – Statistics By Jim

What does a probability of 0.05 mean?

Keywords People Search

Is p 0.01 statistically significant?
“P < 0.05” Might Not Mean What You Think: American Statistical ... - NCBI

What does a 0.001 p-value mean?

The p-value indicates how probable the results are due to chance. p=0.05 means that there is a 5% probability that the results are due to random chance. p=0.001 means that the chances are only 1 in a thousand. The choice of significance level at which you reject null hypothesis is arbitrary.

Keywords People Search

Is p 0.01 statistically significant?
P Value, Statistical Significance and Clinical Significance

Is 0.006 statistically significant?

The p value of 0.006 means that an ARR of 19.6% or more would occur in only 6 in 1000 trials if streptomycin was equally as effective as bed rest. Since the p value is less than 0.05, the results are statistically significant (ie, it is unlikely that streptomycin is ineffective in preventing death).

Keywords People Search

Is p 0.01 statistically significant?
Statistical approaches to uncertainty: p values and confidence intervals …

Is 0.002 statistically significant?

I have been surprised to see that many researchers interpret a result with a risk ratio of 0.59 with a P-value of 0.16 as non-significant or ‘no difference,’ while stating that a risk ratio of 0.83 with a P-value of 0.002 is highly significant. 15 thg 3, 2017

Keywords People Search

What does p-value of 0.001 mean?
Some Facts That You Might Be Unaware of About the P-Value – PMC

Is a low p-value statistically significant?

A p-value measures the probability of obtaining the observed results, assuming that the null hypothesis is true. The lower the p-value, the greater the statistical significance of the observed difference. A p-value of 0.05 or lower is generally considered statistically significant.

Keywords People Search

What does p-value of 0.001 mean?
P-Value Definition – Investopedia

Is p-value of 0.05 significant?

If the p-value is 0.05 or lower, the result is trumpeted as significant, but if it is higher than 0.05, the result is non-significant and tends to be passed over in silence. 8 thg 9, 2015

Keywords People Search

What does p-value of 0.001 mean?
Why the p-value is significant | Tidsskrift for Den norske legeforening

What does p-value 0.1 mean?

Keywords People Search

What is a 1% level of significance?
What is a P-value? – Biosci

What is the difference between 0.01 and 0.05 level of significance?

Different levels of cutoff trade off countervailing effects. Lower levels – such as 0.01 instead of 0.05 – are stricter, and increase confidence in the determination of significance, but run an increased risk of failing to reject a false null hypothesis.

Keywords People Search

What is a 1% level of significance?
A Closer Look at Tests of Significance | Boundless Statistics

Is 0.1 statistically significant?

Significance Levels. The significance level for a given hypothesis test is a value for which a P-value less than or equal to is considered statistically significant. Typical values for are 0.1, 0.05, and 0.01. These values correspond to the probability of observing such an extreme value by chance.

Keywords People Search

What is a 1% level of significance?
Tests of Significance

What is the difference between significance and meaningfulness?

Statistical significance reflects the influence of chance on the outcome, whereas clinical meaningfulness reflects the clinical value of the outcome. 1 thg 12, 2015

Keywords People Search

What is the difference between 0.01 and 0.05 level of significance?
The Difference Between Statistical and Clinical Meaningfulness

What percentage is statistically significant?

5% Statistical hypothesis testing is used to determine whether the result of a data set is statistically significant. Generally, a p-value of 5% or lower is considered statistically significant.

Keywords People Search

What is the difference between 0.01 and 0.05 level of significance?
Statistical Significance Definition – Investopedia

How is Gaussian probability calculated?

The nature of the gaussian gives a probability of 0.683 of being within one standard deviation of the mean. The mean value is a=np where n is the number of events and p the probability of any integer value of x (this expression carries over from the binomial distribution ).

Keywords People Search

Is Gaussian normalized?
Gaussian Distribution Function – Hyperphysics

What is difference between Gaussian and normal distribution?

Keywords People Search

Is Gaussian normalized?
Normal Distribution Definition – Investopedia

What is Gaussian theory?

In probability theory and statistics, a Gaussian process is a stochastic process (a collection of random variables indexed by time or space), such that every finite collection of those random variables has a multivariate normal distribution, i.e. every finite linear combination of them is normally distributed.

Keywords People Search

Is Gaussian normalized?
Gaussian process – Wikipedia

Does parametric mean normally distributed?

Parametric tests are suitable for normally distributed data. Nonparametric tests are suitable for any continuous data, based on ranks of the data values. Because of this, nonparametric tests are independent of the scale and the distribution of the data. 18 thg 5, 2018

Keywords People Search

How do you know if data is Gaussian?
How to Choose Between Parametric & Nonparametric Tests | Alchemer

How do you use Shapiro test in R?

Updating

Keywords People Search

How do you know if data is Gaussian?
Shapiro-Wilk Normality Test in R (Example) | plot & density Functions

How do you calculate Gaussian distribution?

For quick and visual identification of a normal distribution, use a QQ plot if you have only one variable to look at and a Box Plot if you have many. Use a histogram if you need to present your results to a non-statistical public. As a statistical test to confirm your hypothesis, use the Shapiro Wilk test. 13 thg 12, 2019

Keywords People Search

How do you know if data is Gaussian?
6 ways to test for a Normal Distribution — which one to use?

How do you know if data is Gaussian?

Keywords People Search

What is the difference between Gaussian and normal distribution?
How do I know if my data have a normal distribution? – FAQ 2185

Does Gaussian mean normal?

Gaussian distribution (also known as normal distribution) is a bell-shaped curve, and it is assumed that during any measurement values will follow a normal distribution with an equal number of measurements above and below the mean value.

Keywords People Search

What is the difference between Gaussian and normal distribution?
Gaussian Distribution – an overview | ScienceDirect Topics

Why normal distribution is called Gaussian?

The normal distribution is often called the bell curve because the graph of its probability density looks like a bell. It is also known as called Gaussian distribution, after the German mathematician Carl Gauss who first described it.

Keywords People Search

What is the difference between Gaussian and normal distribution?
Introduction to the Normal Distribution (Bell Curve) – Simply Psychology

Is Gaussian distribution discrete or continuous?

Keywords People Search

Is Gaussian random variable continuous?
List of probability distributions – Wikipedia

Is Z distribution continuous?

This bell-shaped curve is used in almost all disciplines. Since it is a continuous distribution, the total area under the curve is one. The parameters of the normal are the mean μ and the standard deviation σ. A special normal distribution, called the standard normal distribution is the distribution of z-scores. 10 thg 8, 2020

Keywords People Search

Is Gaussian random variable continuous?
6: Continuous Random Variables and the Normal Distribution

Is gamma distribution discrete or continuous?

continuous probability distributions In probability theory and statistics, the gamma distribution is a two-parameter family of continuous probability distributions.

Keywords People Search

Is Gaussian random variable continuous?
Gamma distribution – Wikipedia

What is the difference between Poisson and normal distribution?

One difference is that in the Poisson distribution the variance = the mean. In a normal distribution, these are two separate parameters. The value of one tells you nothing about the other. So a Poisson distributed variable may look normal, but it won’t quite behave the same.

Keywords People Search

Is Poisson distribution discrete or continuous?
Differences Between the Normal and Poisson Distributions

What is the probability mass function of Poisson distribution?

The Poisson Distribution probability mass function gives the probability of observing k events in a time period given the length of the period and the average events per time: Poisson distribution for probability of k events in time period. 20 thg 1, 2019

Keywords People Search

Is Poisson distribution discrete or continuous?
The Poisson Distribution and Poisson Process Explained | by Will Koehrsen

Is the distribution a discrete probability distribution?

Is the distribution a discrete probability distribution? Yes, because the sum of the probabilities is equal to 1 and each probability is between 0 and 1, inclusive.

Keywords People Search

Is Poisson distribution discrete or continuous?
STATISTICS 125 – CHAPTER 6.1 Discrete Random Variables – Quizlet

What are the three standard limits in an empirical rule?

The Empirical Rule states that 99.7% of data observed following a normal distribution lies within 3 standard deviations of the mean. Under this rule, 68% of the data falls within one standard deviation, 95% percent within two standard deviations, and 99.7% within three standard deviations from the mean.

Keywords People Search

Is Poisson a Gaussian?
Empirical Rule Definition – Investopedia

Is binomial discrete or continuous?

discrete distribution 4.20. 1 Binomial Distribution. Binomial distribution is a discrete distribution. It is a commonly used probability distribution.

Keywords People Search

Is Poisson a Gaussian?
Binomial Distribution – an overview | ScienceDirect Topics

Is exponential distribution discrete or continuous?

continuous distribution The exponential distribution is the only continuous distribution that is memoryless (or with a constant failure rate). Geometric distribution, its discrete counterpart, is the only discrete distribution that is memoryless.

Keywords People Search

Is Poisson a Gaussian?
Exponential Distribution — Intuition, Derivation, and Applications

What is Bayes theorem and maximum posterior hypothesis?

Recall that the Bayes theorem provides a principled way of calculating a conditional probability. It involves calculating the conditional probability of one outcome given another outcome, using the inverse of this relationship, stated as follows: P(A | B) = (P(B | A) * P(A)) / P(B) 8 thg 11, 2019

Keywords People Search

What is maximum posterior hypothesis in machine learning?
A Gentle Introduction to Maximum a Posteriori (MAP) for Machine …

What is the difference between maximum a posteriori and maximum likelihood hypothesis?

Maximum A Posteriori The difference is that the MAP estimate will use more information than MLE does; specifically, the MAP estimate will consider both the likelihood – as described above – and prior knowledge of the system’s state, X [6]. The MAP estimate, therefore, is a form of Bayesian inference [9]. 18 thg 5, 2020

Keywords People Search

What is maximum posterior hypothesis in machine learning?
MLE vs MAP – Emma Benjaminson

What is the di erence between estimating with MLE and MAP?

The difference between MLE/MAP and Bayesian inference MLE gives you the value which maximises the Likelihood P(D|θ). And MAP gives you the value which maximises the posterior probability P(θ|D). As both methods give you a single fixed value, they’re considered as point estimators. 20 thg 9, 2019

Keywords People Search

What is maximum posterior hypothesis in machine learning?
MLE, MAP and Bayesian Inference – Towards Data Science

What are prior likelihood and posterior distributions?

Keywords People Search

How do you calculate posterior mode?
Prior, likelihood, and posterior – Machine Learning with Spark

How do you interpret posterior?

Point Estimates When q is a continuous-valued variable, as here, the most common Bayesian point estimate is the mean (or expectation) of the posterior distribution, which is called the “posterior mean”. The mean of the Beta(31,71) distribution is 31/(31+71) = 0.3. So we would say “The posterior mean for q is 0.3.” 28 thg 1, 2017

Keywords People Search

How do you calculate posterior mode?
Summarizing and Interpreting the Posterior (analytic)

How do you calculate Bayesian prior?

Bayes’ theorem is really cool. What makes it useful is that it allows us to use some knowledge or belief that we already have (commonly known as the prior) to help us calculate the probability of a related event. … They are: P(B|A) = P(red|4) = 1/2. P(A) = P(4) = 4/52 = 1/13. P(B) = P(red) = 1/2. 5 thg 1, 2018

Keywords People Search

How do you calculate posterior mode?
Probability concepts explained: Bayesian inference for parameter …

What is alpha and beta in gamma distribution?

Keywords People Search

How do you interpret gamma distribution?
Gamma Distribution: Definition, PDF, Finding in Excel – Statistics How To

What is gamma distribution in probability?

Keywords People Search

How do you interpret gamma distribution?
Gamma Distribution Explained | What is Gamma Distribution?

What is the expected value of a gamma distribution?

From the definition of the Gamma distribution, X has probability density function: fX(x)=βαxα−1e−βxΓ(α) From the definition of the expected value of a continuous random variable: E(X)=∫∞0xfX(x)dx. 19 thg 6, 2019

Keywords People Search

How do you interpret gamma distribution?
Expectation of Gamma Distribution – ProofWiki

Is gamma distribution bounded?

The gamma distribution is bounded below by zero (all sample points are positive) and is unbounded from above. It has a theoretical mean of alpha*beta and a theoretical variance of alpha*beta^2 .

Keywords People Search

What is the standard deviation of a gamma distribution?
Gamma distribution – Analytica Wiki

How do you convert gamma distribution to normal distribution?

You can transform random variables from one to another with the inverse CDF method: If γ is Gamma distributed (with some fixed parameters), and F its CDF then F(γ) has uniform(0,1) distribution. Thus Φ−1(F(γ)) has Normal distribution. 6 thg 6, 2015

Keywords People Search

What is the standard deviation of a gamma distribution?
How can you convert a gamma distribution into normal distribution?

What is the value of gamma 1?

To extend the factorial to any real number x > 0 (whether or not x is a whole number), the gamma function is defined as Γ(x) = Integral on the interval [0, ∞ ] of ∫ 0∞t x − 1 e− t dt. Using techniques of integration, it can be shown that Γ(1) = 1.

Keywords People Search

What is the standard deviation of a gamma distribution?
gamma function | Properties, Examples, & Equation | Britannica

What is the difference between gamma and beta distribution?

1 Expert Answer. One significant difference is that the beta distribution is defined on the interval [0, 1], where as the gamma distribution is defined for all non negative values. 31 thg 5, 2020

Keywords People Search

What is beta in gamma distribution?
What is the difference between the Beta and Gamma distribution?

laplace approximation marginal likelihood – The Laplace approximation to a posterior

Watch Video Now

Pictures on the topic laplace approximation marginal likelihood | The Laplace approximation to a posterior

What is the standard deviation of a gamma distribution?

Gamma Distribution Mean γ Range 0 to \infty. Standard Deviation \sqrt{\gamma} Skewness \frac{2} {\sqrt{\gamma}} Kurtosis 3 + \frac{6} {\gamma} 2 hàng khác

Keywords People Search

What is beta in gamma distribution?
1.3.6.6.11. Gamma Distribution

When should you use gamma distribution?

We can use the Gamma distribution for every application where the exponential distribution is used — Wait time modeling, Reliability (failure) modeling, Service time modeling (Queuing Theory), etc. — because exponential distribution is a special case of Gamma distribution (just plug 1 into k). 12 thg 10, 2019

Keywords People Search

What is beta in gamma distribution?
Gamma Distribution — Intuition, Derivation, and Examples

What does beta distribution tell us?

In short, the beta distribution can be understood as representing a probability distribution of probabilities- that is, it represents all the possible values of a probability when we don’t know what that probability is. 20 thg 12, 2014

Keywords People Search

What is alpha and beta in beta distribution?
Understanding the beta distribution (using baseball statistics)

What is β in statistics?

Beta (β) refers to the probability of Type II error in a statistical hypothesis test. Frequently, the power of a test, equal to 1–β rather than β itself, is referred to as a measure of quality for a hypothesis test. 27 thg 12, 2012

Keywords People Search

What is alpha and beta in beta distribution?
Beta – SAGE Research Methods

How do you calculate beta probability?

How do I calculate the expected value in a beta distribution? To determine the expected value of a random variable X following the beta distribution with shape parameters α and β , use the formula: E(X) = α / (α + β) . 8 thg 11, 2021

Keywords People Search

What is alpha and beta in beta distribution?
Beta Distribution Calculator